题目内容
如图，梯形ABCD的中位线EF的长为a，高为h，则图中阴影部分的面积为________
S阴影=
ah
分析：延长AF交DC的延长线于M，则△ABF≌△MCF，易得S阴影=S△DFM，再由同底同高可得S△ADF=S△MDF，即阴影部分的面积等于梯形面积的一半，据此求解即可．
解答：
解：延长AF交DC的延长线于M，则△ABF≌△MCF，
∴AF=FM，S△ABF=S△CMF．
∴S阴影=S△DFM，
∵AF=FM，
∴S△ADF=S△MDF，
∴
，
∵S梯形ABCD=ah，
∴S阴影=ah．
点评：此题主要考查梯形中位线的性质：梯形中位线等于上底和下底和的一半．辅助线的作法是关键．
ah分析：延长AF交DC的延长线于M，则△ABF≌△MCF，易得S阴影=S△DFM，再由同底同高可得S△ADF=S△MDF，即阴影部分的面积等于梯形面积的一半，据此求解即可．
解答：
解：延长AF交DC的延长线于M，则△ABF≌△MCF，∴AF=FM，S△ABF=S△CMF．
∴S阴影=S△DFM，
∵AF=FM，
∴S△ADF=S△MDF，
∴
，∵S梯形ABCD=ah，
∴S阴影=
ah．点评：此题主要考查梯形中位线的性质：梯形中位线等于上底和下底和的一半．辅助线的作法是关键．
练习册系列答案
相关题目
如图，梯形ABCD的对角线交于点O，有以下四个结论：①△AOB∽△COD，②△AOD∽△ACB，③S△DOC：S△AOD=DC：AB，④S△AOD=S△BOC，其中始终正确的有（ ）个．
| A、1 | B、2 | C、3 | D、4 |
14、如图，梯形ABCD的两条对角线交于点E，图中面积相等的三角形共有
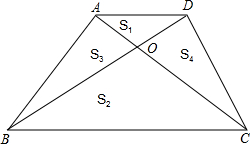如图，梯形ABCD的对角线AC、BD相交于点O，△ADO的面积记作S1，△BCO的面积记作S2，△ABO的面积记作S3，△CDO的面积记作S4，则下列关系正确是（ ）| A、S1=S2 | B、S1×S2=S3×S4 | C、S1+S2=S4+S3 | D、S2=2S3 |
16、如图，梯形ABCD的对角线交于点O，有以下三个结论：
如图，梯形ABCD的面积为34cm2，AE=BF，CE与DF相交于O，△OCD的面积为11cm2，则阴影部分的面积为