题目内容
19. 如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.
如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.(1)求证:BE=CE;
(2)若BD=1,BE=2,求AC的长.
分析 (1)根据等腰三角形的三线合一即可证明.
(2)由△BED∽△BAC,得$\frac{BE}{BA}=\frac{BD}{BC}$,列出方程即可解决问题.
解答 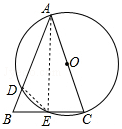 (1)证明:连结AE,如图,
(1)证明:连结AE,如图,
∵AC为⊙O的直径,
∴∠AEC=90°,
∴AE⊥BC,而AB=AC,
∴BE=CE.
(2)连结DE,如图,
∵BE=CE=2,
∴BC=4,
∵∠BED=∠BAC,而∠DBE=∠CBA,
∴△BED∽△BAC,
∴$\frac{BE}{BA}=\frac{BD}{BC}$,即$\frac{2}{BA}=\frac{1}{4}$,
∴BA=8,
∴AC=BA=8.
点评 本题考查圆周角定理、等腰三角形的性质.相似三角形的判定和性质等知识,解题的关键是灵活应用所学知识解决问题,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.20筐胡萝卜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示. 记录如表:
(1)20筐胡萝卜中,最重的一筐比最轻的一筐重5千克;
(2)与标准重量比较,20筐胡萝卜总计超过或不足多少千克?
(3)若胡萝卜每千克售价2元,则出售这20筐胡萝卜可卖多少元?
| 与标准质量的差值 (单位:千克) | -3 | -2 | -1.5 | 0 | 1 | 2 |
| 筐数 | 1 | 4 | 2 | 4 | 1 | 8 |
(2)与标准重量比较,20筐胡萝卜总计超过或不足多少千克?
(3)若胡萝卜每千克售价2元,则出售这20筐胡萝卜可卖多少元?
14.下列那些数是方程x2+x-6=0的根是( )
| A. | -3和2 | B. | -3和-2 | C. | -2和3 | D. | 2和3 |
4.化简$\sqrt{4}$的结果是( )
| A. | 2 | B. | ±2 | C. | $\sqrt{2}$ | D. | ±$\sqrt{2}$ |
11. 如图,△ABC和△DCE都是直角三角形,其中一个三角形是由另一个三角形旋转得到的,下列叙述中错误的是( )
如图,△ABC和△DCE都是直角三角形,其中一个三角形是由另一个三角形旋转得到的,下列叙述中错误的是( )
 如图,△ABC和△DCE都是直角三角形,其中一个三角形是由另一个三角形旋转得到的,下列叙述中错误的是( )
如图,△ABC和△DCE都是直角三角形,其中一个三角形是由另一个三角形旋转得到的,下列叙述中错误的是( )| A. | 旋转中心是点C | |
| B. | 顺时针旋转角是90° | |
| C. | 旋转中心是点B,旋转角是∠ABC | |
| D. | 既可以是逆时针旋转又可以是顺时针旋转 |
 如图,已知直线AB,CD被直线EF所截,若∠A=75°,∠C=105°,∠AEF=60°,则∠EFD的度数为60°.
如图,已知直线AB,CD被直线EF所截,若∠A=75°,∠C=105°,∠AEF=60°,则∠EFD的度数为60°.