题目内容
 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,E为BC中点,则sin∠AEB的值是( )
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,E为BC中点,则sin∠AEB的值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:勾股定理,直角三角形斜边上的中线,勾股定理的逆定理,锐角三角函数的定义
专题:网格型
分析:如图过A作AM⊥BC于M,由于在边长为1的小正方形组成的网格中,△ABC的边长可以利用勾股定理求出,求出高AM和AE,然后利用三角函数的定义即可求解.
解答:解:
过A作AM⊥BC于M,
依题意得
AB=
=
,
AC=
=2
,
BC=
=5,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,
∴S△ABC=
AB×AC=
BC×AM,
∴
×2
=5AM,
∴AM=2,
∴sin∠AEB=
又∵E为BC的中点,
∴AE=CE=BE=
,
∴sin∠AEB=
=
=
,
故选D.

过A作AM⊥BC于M,
依题意得
AB=
| 22+12 |
| 5 |
AC=
| 22+42 |
| 5 |
BC=
| 32+42 |
∴AB2+AC2=BC2,
∴△ABC是直角三角形,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 5 |
| 5 |
∴AM=2,
∴sin∠AEB=
又∵E为BC的中点,
∴AE=CE=BE=
| 5 |
| 2 |
∴sin∠AEB=
| AM |
| AE |
| 2 | ||
|
| 4 |
| 5 |
故选D.
点评:此题主要考查了三角函数的定义,也考查了勾股定理及其逆定理,首先根据图形求出三角形的边长,然后利用勾股定理及其逆定理和三角函数即可解决问题.

练习册系列答案
相关题目
在实数
、0、π、3.1415、-3、
、2.10100110001…中,无理数的个数为( )
| 5 |
| 4 |
| A、2个 | B、3个 | C、4个 | D、5个 |
 如图,A、B、C在⊙O上,若∠BAC=24°,则∠BOC的度数是( )
如图,A、B、C在⊙O上,若∠BAC=24°,则∠BOC的度数是( )| A、12° | B、24° |
| C、48° | D、84° |
下面在平面直角坐标系中所给的四个图象中,是函数图象的是( )
A、 |
B、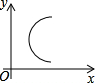 |
C、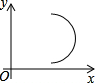 |
D、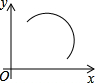 |
 如图,某校一幢教学大楼的顶部竖有一块中考倒计时牌CD.小明在山坡的坡脚A处测得倒计时牌底部D的仰角为60°,沿山坡向上走到B处测得倒计时牌顶部C的仰角为45°.已知山坡AB的坡度i=1:
如图,某校一幢教学大楼的顶部竖有一块中考倒计时牌CD.小明在山坡的坡脚A处测得倒计时牌底部D的仰角为60°,沿山坡向上走到B处测得倒计时牌顶部C的仰角为45°.已知山坡AB的坡度i=1: 一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,AB=3m,已知木箱高BE=
一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,AB=3m,已知木箱高BE=