题目内容
5.先化简代数式:$\frac{a•(a-1)}{{{a^2}-4}}÷[\frac{a}{a+2}+\frac{1}{(a+2)(a-2)}]$,再求当a=$\sqrt{2}$-1时代数式的值.分析 先根据分式混合运算的法则把原式进行化简,再把a的值代入进行计算即可.
解答 解:原式=$\frac{a(a-1)}{(a-2)(a+2)}$÷$\frac{a(a-2)+1}{(a-2)(a+2)}$
=$\frac{a(a-1)}{(a-2)(a+2)}$÷$\frac{{a}^{2}-2a+1}{(a-2)(a+2)}$
=$\frac{a(a-1)}{(a-2)(a+2)}$•$\frac{(a-2)•(a+2)}{{(a-1)}^{2}}$
=$\frac{a(a-1)}{(a-2)(a+2)}$•$\frac{(a-2)×(a+2)}{{(a-1)}^{2}}$
=$\frac{a}{a-1}$,
当a=$\sqrt{2}$-1时,原式=-$\frac{\sqrt{2}}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
20.-2的绝对值是( )
| A. | 2 | B. | $\sqrt{2}$ | C. | $±\sqrt{2}$ | D. | $\frac{1}{2}$ |
14.下列各图中,经过折叠能围成立方体的是( )
| A. | 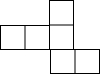 | B. | 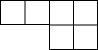 | C. | 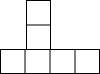 | D. | 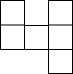 |