题目内容
 如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.(1)填空:∠ABC=
(2)判断:△ABC与△DEF是否相似?并说明理由.
考点:相似三角形的判定,勾股定理
专题:网格型
分析:(1)根据已知条件,结合网格可以求出∠ABC的度数,根据△ABC和△DEF的顶点都在边长为1的小正方形的顶点上,利用勾股定理即可求出线段BC的长;
(2)根据相似三角形的判定定理,夹角相等,对应边成比例即可证明△ABC与△DEF相似.
(2)根据相似三角形的判定定理,夹角相等,对应边成比例即可证明△ABC与△DEF相似.
解答:(1)解:∠ABC=∠DEF=90°+45°=135°,
BC=
=2
.
DE=
=
故答案为:135;135;2
;
.
(2)△ABC∽△DEF.
证明:∵在4×4的正方形方格中,
∠ABC=∠DEF=135°,
∴∠ABC=∠DEF.
∵AB=2,BC=2
,FE=2,DE=
,
∴
=
=
,
=
=
.
∴
=
,
∴△ABC∽△DEF.
BC=
| 22+22 |
| 2 |
DE=
| 12+12 |
| 2 |
故答案为:135;135;2
| 2 |
| 2 |
(2)△ABC∽△DEF.
证明:∵在4×4的正方形方格中,
∠ABC=∠DEF=135°,
∴∠ABC=∠DEF.
∵AB=2,BC=2
| 2 |
| 2 |
∴
| AB |
| DE |
| 2 | ||
|
| 2 |
| BC |
| FE |
2
| ||
| 2 |
| 2 |
∴
| AB |
| DE |
| BC |
| FE |
∴△ABC∽△DEF.
点评:此题主要考查学生对勾股定理和相似三角形的判定的理解和掌握,解答此题的关键是认真观察图形,得出两个三角形角和角,边和边的关系.

练习册系列答案
相关题目
只用两枚钉子就把一根木条固定在墙上,下列语句能解释这个原理的是( )
| A、木条是直的 |
| B、两点确定一线 |
| C、过一点可以画出无数条直线 |
| D、两点之间线段最短 |
若(p-2)x2+3x+p2-p=0是关于x的一元二次方程,则( )
| A、p=2 | B、p≠0 |
| C、p>2 | D、p≠2 |
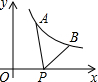 如图,已知A(
如图,已知A( 解不等式组,并把解集在数轴上表示出来.
解不等式组,并把解集在数轴上表示出来. 如图,一次函数y=kx+b的图象与y轴交于点(0,1),则关于x的不等式kx+b>1的解集是
如图,一次函数y=kx+b的图象与y轴交于点(0,1),则关于x的不等式kx+b>1的解集是