题目内容
【题目】已知:如图,以等边![]() 的边
的边![]() 为直径作
为直径作![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
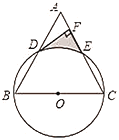
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若等边![]() 的边长为8,求由
的边长为8,求由![]() 、
、![]() 、
、![]() 围成的阴影部分面积.
围成的阴影部分面积.
【答案】(1)详见解析;(2)6![]() ﹣
﹣![]() .
.
【解析】
(1)连接CD、OD,先利用等腰三角形的性质证AD=BD,再证OD为△ABC的中位线得DO∥AC,根据DF⊥AC可得结论;
(2)连接OE,作OG⊥AC,求出EF、DF的长及∠DOE的度数,根据S阴影=S梯形EFDO﹣S扇形DOE计算可得.
解:(1)连接CD、OD,
∵BC是⊙O的直径,
∴∠CDB=90°,即CD⊥AB,
又∵△ABC是等边三角形,
∴AD=BD,
∵BO=CO,
∴DO是△ABC的中位线,
∴OD∥AC,
∵DF⊥AC,
∴DF⊥OD,
∴DF是⊙O的切线;
(2)连接OE,作OG⊥AC于点G,
∴∠OGF=∠DFG=∠ODF=90°,
∴四边形OGFD是矩形,
∴FG=OD=4,
∵OC=OE=OD=OB,且∠ACB=∠B=60°,
∴△OBD和△OCE均为等边三角形,
∴∠BOD=∠COE=60°,CE=OC=4,
∴EG=![]() CE=2,DF=OG=OCsin60°=2
CE=2,DF=OG=OCsin60°=2![]() ,∠DOE=60°,
,∠DOE=60°,
∴EF=FG﹣EG=2,
∴S阴影=S梯形EFDO﹣S扇形DOE=![]() ×(2+4)×2
×(2+4)×2![]() ﹣
﹣![]() =6
=6![]() ﹣
﹣![]() .
.


 巧学巧练系列答案
巧学巧练系列答案【题目】某校共有200名学生,为了解本学期学生参加公益劳动的情况,收集了他们参加公益劳动时间(单位:小时)等数据,以下是根据数据绘制的统计图表的一部分.
学 生 类 型 人数 时间 |
|
|
|
|
| |
性别 | 男 | 7 | 31 | 25 | 30 | 4 |
女 | 8 | 29 | 26 | 32 | 8 | |
学段 | 初中 | 25 | 36 | 44 | 11 | |
高中 | ||||||

下面有四个推断:
①这200名学生参加公益劳动时间的平均数一定在24.5-25.5之间
②这200名学生参加公益劳动时间的中位数在20-30之间
③这200名学生中的初中生参加公益劳动时间的中位数一定在20-30之间
④这200名学生中的高中生参加公益劳动时间的中位数可能在20-30之间
所有合理推断的序号是( )
A. ①③B. ②④C. ①②③D. ①②③④