题目内容
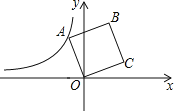
【题目】如图,在平面直角坐标系中,正方形ABCO的顶点O在坐标远点,点B的坐标为(1,4),点A在第二象限,反比例函数![]() 的图像经过点A则K的值是()
的图像经过点A则K的值是()
A.-2B.-4C.-8D.![]()
【答案】D
【解析】
作AD⊥x轴于D,CE⊥x轴于E,先通过证得△AOD≌△OCE得出AD=OE,OD=CE,设A(x,![]() ),则C(
),则C(![]() ,-x),根据正方形的性质求得对角线,解得F的坐标,根据直线OB的解析式,设直线AC的解析式为:y=-
,-x),根据正方形的性质求得对角线,解得F的坐标,根据直线OB的解析式,设直线AC的解析式为:y=-![]() x+b,代入交点坐标求得解析式,然后把A,C的坐标代入即可求得k的值.
x+b,代入交点坐标求得解析式,然后把A,C的坐标代入即可求得k的值.
解:作AD⊥x轴于D,CE⊥x轴于E
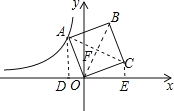
∵∠AOC=90°,
∴∠AOD+∠COE=90°,
∵∠AOD+∠OAD=90°,
∴∠OAD=∠COE,
在△AOD和△OCE中,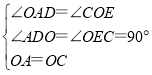 ,
,
∴△AOD≌△OCE(AAS),
∴AD=OE,OD=CE,
∵点B的坐标为(1,4),
∴OB=![]() =
=![]() ,
,
直线OB为:y=4x,
∵AC和OB互相垂直平分,
∴它们的交点F的坐标为(![]() ,2),
,2),
设直线AC的解析式为:y=-![]() x+b,
x+b,
代入(![]() ,2),得,2=-
,2),得,2=-![]() ×
×![]() +b,解得b=
+b,解得b=![]() ,
,
直线AC的解析式为:y=-![]() x+
x+![]() ,
,
把A(x,![]() ),C(
),C(![]() ,-x),代入得
,-x),代入得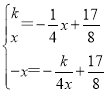 ,解得k=
,解得k=![]() .
.
故选:D.

练习册系列答案
相关题目