题目内容
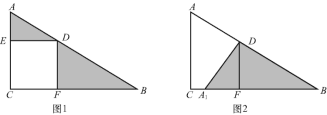
【题目】如图,在平面直角坐标系中,![]() ,P为x轴正半轴一动点,BC平分
,P为x轴正半轴一动点,BC平分![]() ,PC平分
,PC平分![]() ,OD平分
,OD平分![]()
![]() 求
求![]() 的度数;
的度数;
![]() 求证:
求证:![]() ;
;
![]() 在运动中,
在运动中,![]() 的值是否变化?若发生变化,说明理由;若不变,求其值.
的值是否变化?若发生变化,说明理由;若不变,求其值.

【答案】![]() 30°;
30°;![]() 证明见解析;
证明见解析;![]() 不变,105°.
不变,105°.
【解析】
(1)在Rt△AOB中根据已知和两锐角互余的性质即可求出∠BAO的度数;
(2)根据外角的性质表示出∠C,得到∠C与∠OAP之间的数量关系;
(3)根据对顶角相等,分别表示出∠C和∠D,得到∠C+∠D的值.
![]() ∵∠ABO+∠BAO+∠AOB=180°,∠AOB=90°,∠ABO=2∠BAO,
∵∠ABO+∠BAO+∠AOB=180°,∠AOB=90°,∠ABO=2∠BAO,
∴2∠BAO+∠BAO+90°=180°,
∴∠BAO=30°;
![]() ∵∠CBP=
∵∠CBP=![]() ∠ABO,∠ABO=2∠BAO,∠BAO=30°,
∠ABO,∠ABO=2∠BAO,∠BAO=30°,
∴∠CBP=30°,
∵∠CPF=∠C+∠CBP,∠APF=∠OAP+∠AOP,∠CPF=![]() ∠APF,
∠APF,
∴∠C+∠CBP=![]() (∠OAP+∠AOP),
(∠OAP+∠AOP),
∵∠AOP=90°,
∴∠C+30°=![]() (∠OAP+90°)=
(∠OAP+90°)=![]() ∠OAP+45°,
∠OAP+45°,
∴∠C=15°+![]() ∠OAP;
∠OAP;
![]() 不变,
不变,
∵∠D+∠DOP+∠OPD=180°,∠DOP=![]() ∠EOF=
∠EOF=![]() ×90°=45°,
×90°=45°,
∴∠D+45°+∠OPD=180°,
∵∠OPD=∠C+∠CBP,
∴∠D+45°+∠C+∠CBP=180°,
∵∠CBP=30°,
∴∠D+∠C=180°-45°-∠CBP=135°-30°=105°,
∴∠D+∠C=105°,保持不变.

练习册系列答案
相关题目