题目内容
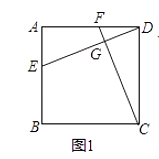
【题目】如图,长方形ABCD,AB=CD=4,BC=AD=8,∠A=∠B=∠C=∠D=90°,E为CD边的中点,P为长方形ABCD边上的动点,动点P从A出发,沿着A B C E运动到E点停止,设点P经过的路程为![]() ,APE的面积为
,APE的面积为![]() .
.
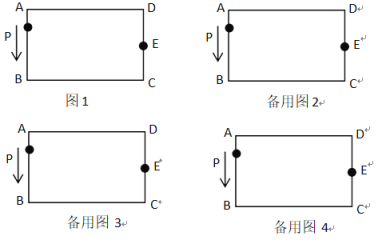
(1)当![]() 时,在图1中画出草图,并求出对应
时,在图1中画出草图,并求出对应![]() 的值;
的值;
(2)利用备用图画出草图,写出![]() 与
与![]() 之间的关系式.
之间的关系式.
【答案】(1)15;(2)①当0≤x≤4时,y=4x;②当4<x≤12时,y=20-x;③当12<x≤14时,y=56-4x
【解析】
(1)先根据题意画出草图,再利用三角形面积求法S△APE=S长方形ABCD-S△APB-S△PCE-S△ADE得出答案即可;
(2)分3种情况来解答,利用当0≤x≤4时,当4<x≤12时,当12<x≤14时,分别求出y与x的函数关系式即可.
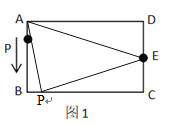
(1)当![]() 时,点P在BC边上,如图1,
时,点P在BC边上,如图1,
∵长方形ABCD,AB=CD=4,BC=AD=8,∠A=∠B=∠C=∠D=90°,E为CD边的中点,
∵x=5
∴BP=x-4=1,CP=12-x=7,CE=ED=2
∴S△APE=S长方形ABCD-S△APB-S△PCE-S△ADE
=8×4-![]() ×4×1-
×4×1-![]() ×7×2-
×7×2-![]() ×2×8
×2×8
=32-2-7-8
=15
∴y=15
(2)分3种情况来讨论,
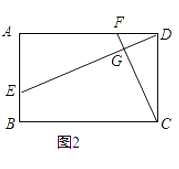
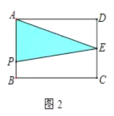
①当0≤x≤4时,如图2,AP=x,
S△APE=![]() ·AP·BC=
·AP·BC=![]() ·x·8=4x
·x·8=4x
∴y=4x
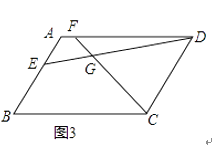
②当4<x≤12时,如图3,BP=x-4,PC=12-x,
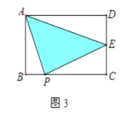
S△APE=S长方形ABCD-S△APB-S△PCE-S△ADE
=4×8-![]() ×(x-4) ×4-
×(x-4) ×4-![]() ×2×(12-x)-
×2×(12-x)- ![]() ×2×8
×2×8
=32-2x+8-12+x-8
=20-x
∴y=20-x
③当12<x≤14时,如图4,
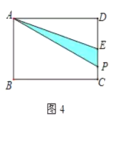
PE=4+8+2-x=14-x
S△AEP=![]() ·PE·8=
·PE·8=![]() ×8×(14-x)=56-4x
×8×(14-x)=56-4x
∴y=56-4x
综上所述:①当0≤x≤4时,y=4x;②当4<x≤12时,y=20-x;③当12<x≤14时,y=56-4x

 导学全程练创优训练系列答案
导学全程练创优训练系列答案