题目内容
标有﹣3，﹣2，4的三张不透明的卡片，除正面写有不同的数字外，其余的值都相同，将这三张卡片背面朝上洗匀后，第一次从中随机抽取一张，并把这张卡片标有的数字记为二次函数解析式y=a（x﹣k）2+b的k值，第二次从余下的两张卡片中再抽取一张，上面标有的数字记为二次函数解析式的b值．
（1）写出k为负数的概率；
（2）求二次函数y=a（x﹣k）2+b的图象上顶点在双曲线y=﹣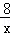
上的概率．（用树状图或列举法求解）
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
B．
C．
D．
提出问题：当x＞0时如何求函数y=x+
的最大值或最小值？
分析问题：前面我们刚刚学过二次函数的相关知识，知道求二次函数的最值时，我们可以利用它的图象进行猜想最值，或利用配方可以求出它的最值．
例如我们求函数y=x﹣2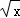
（x＞0）的最值时，就可以仿照二次函数利用配方求最值的方法解决问题；y=x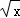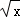﹣2=（
）2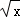﹣2﹣2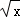+1﹣1=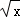（﹣1）2﹣1即当x=1时，y有最小值为﹣1
解决问题
借鉴我们已有的研究函数的经验，探索函数y=x+
（x＞0）的最大（小）值．
（1）实践操作：填写下表，并用描点法画出函数y=x+（x＞0）的图象：
x | … |
|
|
| 1 | 2 | 3 | 4 | … |
y | … | … |
（2）观察猜想：观察该函数的图象，猜想
当x= 时，函数y=x+
（x＞0）有最 值（填“大”或“小”），是 ．
（3）推理论证：利用上述例题，请你尝试通过配方法求函数y=x+（x＞0）的最大（小）值，以证明你的猜想．知识能力运用：直接写出函数y=﹣2x﹣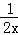
（x＞0）当x= 时，该函数有最 值（填“大”或“小”），是 ．
，AE⊥EF，CF⊥EF，EF=CF，则正方形的边长为 ．
B．
C．
D．