题目内容
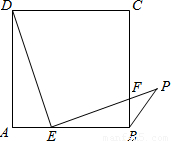
如图，D是AB上的一点，DF交AC于点E，AE=CE，FC∥AB．
求证：DE=FE．
证明：
∵FC∥AB
∴∠FCE=∠DAE，
在△CFE和△ADE中
∴△CFE≌△ADE（ASA），
∴DE=FE．
分析：根据平行线性质得出∠FCE=∠DAE，根据ASA证△CFE≌△ADE，根据全等三角形的性质推出即可．
点评：本题考查了平行线的性质和全等三角形的性质和判定，注意：两直线平行，内错角相等，全等三角形的判定定理有SAS，ASA，AAS，SSS，全等三角形的对应边相等．
∵FC∥AB∴∠FCE=∠DAE，
在△CFE和△ADE中
∴△CFE≌△ADE（ASA），
∴DE=FE．
分析：根据平行线性质得出∠FCE=∠DAE，根据ASA证△CFE≌△ADE，根据全等三角形的性质推出即可．
点评：本题考查了平行线的性质和全等三角形的性质和判定，注意：两直线平行，内错角相等，全等三角形的判定定理有SAS，ASA，AAS，SSS，全等三角形的对应边相等．
练习册系列答案
相关题目
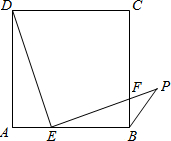（2012•北京二模）已知：如图，BP是正方形ABCD的一条外角平分线，点E在AB边上，EP⊥ED，EP交BC边于点F．
（2012•铁岭）如图，在斜坡AB上有一棵树BD，由于受台风影响而倾斜，恰好与坡面垂直，在地面上C点处测得树顶部D的仰角为60°，测得坡角∠BAE=30°，AB=6米，AC=4米．求树高BD的长是多少米？（结果保留根号）
（2013•南岗区一模）如图，E是AB边上的中点，将△ABC沿过E的直线折叠，使点A落在BC上F处，折痕交边AC于点D，若BC=100，则折痕DE的长度是（ ）
