题目内容
18. 已知:A、B、C是一直线上顺次三点,并且BC=90.
已知:A、B、C是一直线上顺次三点,并且BC=90.(1)若M是AB的中点,N是AC的中点,求MN的长;
(2)若M是AB的中点,两个动点E、F分别从M,C同时出发,E向右行驶,速度为2个单位/秒,F向左行驶,速度为3个单位/秒,如果它们相遇处离B点6个单位,求AB的长;
(3)若P、Q两动点都从A点出发,同时向右匀速行驶,P点速度为2个单位/秒,Q点的速度比P点快,Q点到达B点时间比P点早20秒,到达C点时间比P点早50秒,求Q点运动速度.
分析 (1)设AB=x,根据M是AB的中点、N是AC的中点,即可找出AM、AN的长,二者做差即可得出结论;
(2)设AB的长度为s个单位,相遇的时间为t秒,根据“时间=路程÷速度和,它们相遇处离B点6个单位,”即可列出关于s、t的二元一次方程组,解之即可得出AB的长度;
(3)设点Q的运动速度为v个单位/秒,根据时间=路程÷速度结合“P、Q点从B点出发,Q点到达B点时间比P点早30秒”即可得出关于v的分式方程,解之经检验后即可得出结论.
解答 解:(1)设AB=x,
∵M是AB的中点,N是AC的中点,
∴AM=$\frac{1}{2}$AB=$\frac{1}{2}$x,AN=$\frac{1}{2}$AC=$\frac{1}{2}$(x+90),
∴MN=AN-AM=45.
(2)设AB的长度为s个单位,相遇的时间为t秒,
根据题意,得:$\left\{\begin{array}{l}{(2+3)t=\frac{1}{2}s+90}\\{|3t-90|=6}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{s}_{1}=140}\\{{t}_{1}=32}\end{array}\right.$,$\left\{\begin{array}{l}{{s}_{2}=100}\\{{t}_{2}=28}\end{array}\right.$,
∴AB的长度为140个单位或者100个单位.
(3)设点Q的运动速度为v个单位/秒,
根据题意,得:$\frac{90}{2}$-$\frac{90}{v}$=50-20,
解得:v=6,
经检验,v=6是方程的解.
答:Q点运动速度为6个单位/秒.
点评 本题考查了两点间的距离、列代数式、二元一次方程组的应用以及分式方程的应用,根据数量关系列出方程是解题的关键.

 如图,在△ABC外作两个大小不同的等腰直角三角形,其中∠DAB=∠CAE=90°,AB=AD,AC=AE,连结DC、BE交于F点.
如图,在△ABC外作两个大小不同的等腰直角三角形,其中∠DAB=∠CAE=90°,AB=AD,AC=AE,连结DC、BE交于F点.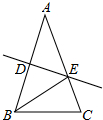 如图,在△ABC中,边AB的垂直平分线交AC于E,△ABC与△BEC的周长分别为24
如图,在△ABC中,边AB的垂直平分线交AC于E,△ABC与△BEC的周长分别为24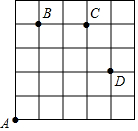 如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走均为正,向下向左走均为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.
如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走均为正,向下向左走均为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.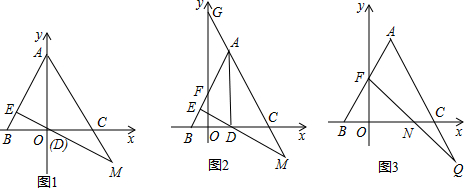
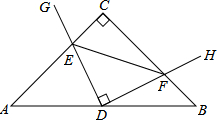 在Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG、DH分别与边AC、BC交于E,F两点.下列结论:
在Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG、DH分别与边AC、BC交于E,F两点.下列结论: 如图,D是△ABC的边AB上的一点,BD=$\frac{4}{3}$,AB=3,BC=2
如图,D是△ABC的边AB上的一点,BD=$\frac{4}{3}$,AB=3,BC=2