题目内容
9. 如图,抛物线y=ax2+bx-4与x轴交于A(-4,0)、B(2,0)两点,与y轴交于点C,连接AC,BC.
如图,抛物线y=ax2+bx-4与x轴交于A(-4,0)、B(2,0)两点,与y轴交于点C,连接AC,BC.(1)求该抛物线的解析式;
(2)若点P是x轴上的一动点,且位于AB之间,过点P作PE∥AC,交BC于E,连接CP,设P点横坐标为x,△PCE的面积为S,请求出S关于x的解析式,并求△PCE面积的最大值;
(3)点为D(-2,0),若点M是线段AC上一动点,是否存在M点,能使△OMD是等腰三角形?若存在,请直接写出M点的坐标;若不存在,请说明理由.
分析 (1)将A、B两点坐标代入解析式直接求出a、b即可;
(2)设出P点横坐标,由于PE∥AC,则△BPE和△BAC相似,根据面积比是相似比的平方得出△BPE的面积表达式,用△PCB的面积减去△BPE的面积就是S,再利用配方法求最值即可;
(3)分两种情况讨论:①DO=DM;②MD=MO.
解答 解:(1)把点A(-4,0),B(2,0)分别代入中,得:$\left\{\begin{array}{l}{16a-4b-4=0}\\{4a+2b-4=0}\end{array}\right.$,
∴a=$\frac{1}{2}$,b=1,
∴这个二次函数解析式为$y=\frac{1}{2}{x}^{2}+x-4$,C(0,-4);
(2)设P点坐标为(x,0),则BP=2-x,S△ABC=$\frac{1}{2}AB•OC=\frac{1}{2}×6×4=12$
∵PE∥AC,
∴∠BPE=∠BAC,∠BEP=∠BCA,
∴△BPE∽△BAC,
∴$\frac{{S}_{△BPE}}{{S}_{△BAC}}$=($\frac{BP}{BA}$)2,即:$\frac{{S}_{△BPE}}{12}$=($\frac{2-x}{6}$)2,
∴${S}_{△BPE}=\frac{1}{3}(2-x)^{2}$,
又∵${S}_{△BCP}=\frac{1}{2}(2-x)×4=2(2-x)$,
∴S△PCE=S△BCP-S△BPE=2(2-x)-$\frac{1}{3}(2-x)^{2}$=$-\frac{1}{3}(x+1)^{2}+3$,
∴x=-1时,△PCE面积有最大值为3;
(3)存在M点.①如图,过点D作DM垂直x轴交AC于M,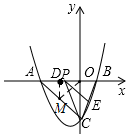
∵A(-4,0),C(-4,0),
∴DM=AD=2=DO,
∴M(-2,-2);
②如图,设DO的中垂线交AC于点M,则MD=MO,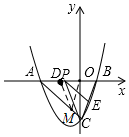
由A、C两点坐标可知AC的解析式为y=-x-4,
将x=-1代入可得y=-3,
∴M(-1,-3).
综上所述,点M的坐标为(-1,-3)或(-2,-2).
点评 本题是二次函数综合题,主要考查了待定系数法求二次函数解析式,相似三角形的判定与性质,配方法求二次函数最值,待定系数法求一次函数解析式,等腰三角形等知识点,综合性较强,难度中等.对于第三问,分类讨论是解答的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | -2 | B. | -7 | C. | 5 | D. | 1 |
| A. | x+2 | B. | x-1 | C. | $\frac{1}{x+2}$ | D. | x-2 |
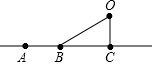 已知如图,则下列叙述不正确的是( )
已知如图,则下列叙述不正确的是( )| A. | 点O不在直线AC上 | B. | 图中共有5条线段 | ||
| C. | 射线AB与射线BC是指同一条射线 | D. | 直线AB与直线CA是指同一条直线 |
| A. | 同位角相等 | B. | 任意三角形的外角一定大于内角 | ||
| C. | 多边形的内角和等于180° | D. | 同角或等角的余角相等 |
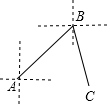 如图所示,一艘船在海上从A点出发,沿东北方向航行至点B,再从B点出发沿南偏东20°方向行至点C,则∠ABC的度数是( )
如图所示,一艘船在海上从A点出发,沿东北方向航行至点B,再从B点出发沿南偏东20°方向行至点C,则∠ABC的度数是( )| A. | 45° | B. | 65° | C. | 75° | D. | 90° |
 如图是水滴进玻璃容器的示意图(滴水速度不变),下列的图是容器中水高度随滴水时间变化的图象,在下列选项中,哪个图能是(a)的图象( )
如图是水滴进玻璃容器的示意图(滴水速度不变),下列的图是容器中水高度随滴水时间变化的图象,在下列选项中,哪个图能是(a)的图象( )


