题目内容
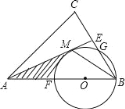
如图,在△ABC中,AB=AC,E是BC中点,点O在AB上,以OB为半径的⊙O经过点AE上的一点M,分别交AB,BC于点F,G,连BM,此时∠FBM=∠CBM.
(1)求证:AM是⊙O的切线;
(2)当BC=6,OB:OA=1:2 时,求 ,AM,AF围成的阴影部分面积.
,AM,AF围成的阴影部分面积.
练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
题目内容
如图,在△ABC中,AB=AC,E是BC中点,点O在AB上,以OB为半径的⊙O经过点AE上的一点M,分别交AB,BC于点F,G,连BM,此时∠FBM=∠CBM.
(1)求证:AM是⊙O的切线;
(2)当BC=6,OB:OA=1:2 时,求 ,AM,AF围成的阴影部分面积.
,AM,AF围成的阴影部分面积.

 一线名师权威作业本系列答案
一线名师权威作业本系列答案