Question

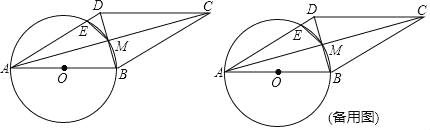
【题目】如图，四边形ABCD是⊙O的内接四边形，AC为直径，点B是弧AC的中点，若AC＝7，BD＝6，则由四个弓形组成的阴影部分的面积为_____．

Answer 1

【答案】π﹣18

【解析】

过A作AN⊥BD于N，过C作CM⊥BD于M，得到∠ANB＝∠BMC＝90°，根据圆周角定理得到∠ABC＝∠ADC＝90°，根据全等三角形的性质得到AN＝BM，BN＝CM，得到CM+AN＝BN+DN＝BD＝6，根据圆和三角形的面积公式即可得到结论．

过A作AN⊥BD于N，过C作CM⊥BD于M，

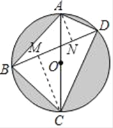
则∠ANB＝∠BMC＝90°，

∵AC为直径，

∴∠ABC＝∠ADC＝90°，

∵点B是弧AC的中点，

∴∠ADB＝∠CDB＝∠BAC＝∠ACB＝45°，

∴∴AB＝BC，∠DAC＝∠BAN＝45°+∠CAN，

∵∠DAC＝∠CBD，

∴∠CBM＝∠BAN，

在△ABN与△BCM中，

，

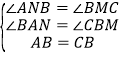∴△ABN≌△BCN（AAS），

∴AN＝BM，BN＝CM，

∵AN＝DN，

∴CM+AN＝BN+DN＝BD＝6，

∴S四边形ABCD＝S△ABD+S△CBD＝BDBD＝18，

∴四个弓形组成的阴影部分的面积＝（）2π﹣18＝π﹣18

故答案为：π﹣18．