题目内容
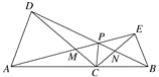
【题目】如图,点C为线段AB上任意一点(不与A、B两点重合),分别以AC、BC为一腰在AB的同侧作等腰△ACD和等腰△BCE,CA=CD,CB=CE,∠ACD与∠BCE都是锐角且∠ACD=∠BCE,连接AE交CD于点M,连接BD交CE于点N,AE与BD交于点P,连接PC.
(1)求证:△ACE≌△DCB;
(2)请你判断△AMC与△DMP的形状有何关系,并说明理由.
【答案】(1)见解析;(2)见解析.
【解析】
(1)证明∠ACE=∠DCB,根据“SAS”证明全等;
(2)由(1)得∠CAM=∠PDM,又∠AMC=∠DMP,所以两个三角形相似.
(1)证明 ∵∠ACD=∠BCE,
∴∠ACD+∠DCE=∠BCE+∠DCE,
∴∠ACE=∠DCB,
又∵CA=CD,CE=CB,
在△ACE和△DCB中,

∴△ACE≌△DCB(SAS).
(2)解 △AMC∽△DMP.
理由:∵△ACE≌△DCB,
∴∠CAE=∠CDB,
又∵∠AMC=∠DMP,
∴△AMC∽△DMP.

练习册系列答案
相关题目
【题目】“十九大”报告提出了我国将加大治理环境污染的力度,还我青山绿水,其中雾霾天气让环保和健康问题成为焦点,为了调查学生对雾霾天气知识的了解程度,某校在全校学生中抽取400名同学做了一次调查,根据调查统计结果,绘制了不完整的一种统计图表.
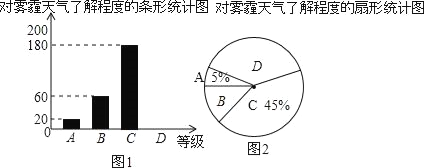
对雾霾了解程度的统计表
对雾霾的了解程度 | 百分比 |
A.非常了解 | 5% |
B.比较了解 | m |
C.基本了解 | 45% |
D.不了解 | n |
请结合统计图表,回答下列问题:
(1)统计表中:m= ,n= ;
(2)请在图1中补全条形统计图;
(3)请问在图2所示的扇形统计图中,D部分扇形所对应的圆心角是多少度?