题目内容

将一个面积为4的正方形按下列顺序折叠，然后将最后折叠的纸片沿虚线（中位线）剪去上方的小三角形，将剩下部分展开所得图形的面积是

A.
$数学公式$
B.
1
C.
2
D.
3

D
分析：根据中位线定理，沿中位线减去小三角形，小三角形的面积与原三角形面积之比为 $\text{[math]}$ ，所以剩下部分的面积是原图面积的 $\text{[math]}$ ．
解答：∵面积为4的正方形折叠以后展开面积不变，∴若把最后折叠成的三角形展开后面积仍为4．
沿中位线减去小三角形，小三角形的面积与原三角形面积之比为 $\text{[math]}$ ，故剩下部分展开所得图形的面积是 $\text{[math]}$ ×4=3．
故选D．
点评：解答此题的关键是要明白经过翻折变换的图形展开后与原图形的面积相等．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

如图，在平面直角坐标系中，直线y=-x-5交x轴于A，交y轴于B，点P（0，-1），D是线段AB上一动点，DC⊥y轴于点C，反比例函数y=

的图象经过点D．
（1）若C为BP的中点，求k的值．

（2）DH⊥DC交OA于H，若D点的横坐标为x，四边形DHOC的面积为y，求y与x之间的函数关系式．

（3）将直线AB沿y轴正方向平移a个单位（a＞5），交x轴、y轴于E、F点，G为y轴负半轴上一点，G（0，-a+5），点M、N以相同的速度分别从E、G两点同时出发，沿x轴、y轴向点O运动（不到达O点），同时静止，连接并延长FM交EN于K，连接OK、MN，当M、N两点在运动过程中以下两个结论：①∠EFM=∠MNK；②∠FMO=∠OKN，其中只有一个结论是正确的，请判断并证明你的结论．

如图所示，在直角坐标系中放置一个边长为1的正方形ABCD，将正方形ABCD沿x轴的正方向无滑动的在x轴上滚动，当点A离开原点后第一次落在x轴上时，点A运动的路径线与x轴围成的面积为

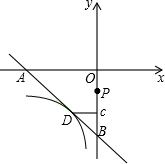
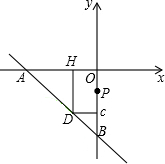
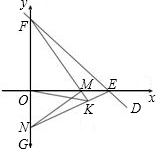
（2013•恩施州）如图所示，在直角坐标系中放置一个边长为1的正方形ABCD，将正方形ABCD沿x轴的正方向无滑动的在x轴上滚动，当点A离开原点后第一次落在x轴上时，点A运动的路径线与x轴围成的面积为（　　）

如图（1），已知，矩形ABCD的边AD=3，对角线长为5，将矩形ABCD置于直角坐标系内，点C与原点O重合，且反比例函数的图象的一个分支位于第一象限．
①求图（1）中，点A的坐标是多少？
②若矩形ABCD从图（1）的位置开始沿x轴的正方向移动，每秒移动1个单位，1秒后点A刚好落在反比例函数的图象上，如图（2），求反比例函数的表达式．
③矩形ABCD继续向x轴的正方向移动，AB、AD与反比例函数图象分别交于P、Q两点，如图（3），设移动总时间为t（1＜t＜5），分别写出△PBC的面积S₁、△QDC的面积S₂与t的函数关系式，并求当t为何值时，S₂=

如图（1）已知，矩形ABDC的边AC=3，对角线长为5，将矩形ABDC置于直角坐系内，点D与原点O重合．且反比例函数y=

的图象的一个分支位于第一象限．
（1）求点A的坐标；
（2）若矩形ABDC从图（1）的位置开始沿x轴的正方向移动，每秒移动1个单位，1秒后点A刚好落在反比例函数y=

的图象的图象上，求k的值；
（3）矩形ABCD继续向x轴的正方向移动，AB、AC与反比例函数图象分别交于P、Q如图（2），设移动的总时间为t（1＜t＜5），分别写出△BPD的面积S₁、△DCQ的面积S₂与t的函数关系式；
（4）在（3）的情况下，当t为何值时，S₂=