题目内容
在梯形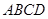 中,
中,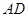 ∥
∥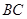 ,
,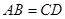 ,
,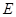 为
为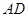 中点.
中点.
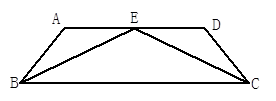
(1)求证: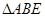 ≌
≌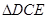 .(2)若
.(2)若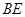 平分
平分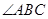 ,且
,且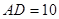 ,求
,求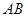 的长.
的长.
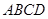 中,
中,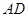 ∥
∥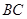 ,
,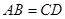 ,
, 为
为 中点.
中点.
(1)求证:
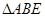 ≌
≌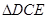 .(2)若
.(2)若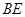 平分
平分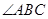 ,且
,且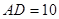 ,求
,求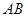 的长.
的长.(1)证明见解析(2)5
证明:(1)∵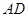 ∥
∥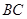 ,
,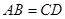 ,∴梯形
,∴梯形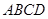 为等腰梯形,∴
为等腰梯形,∴ .
.
又∵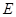 为
为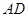 中点,∴
中点,∴ .
.
在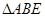 与
与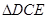 中,
中,
 , ∴
, ∴ …………(4分)
…………(4分)
(2)∵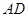 ∥
∥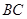 ,∴
,∴ .
.
又∵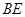 平分
平分 ,∴
,∴ ,
,
∴ ,∴
,∴ .
.
又∵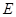 为
为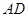 中点,
中点,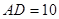 ,
,
∴ .………………………………(8分)
.………………………………(8分)
(1)根据等腰梯形的性质可得∠BAE=∠CDE,再根据SAS即可证明;
(2)根据角平分线的定义和平行线的性质即可发现等腰三角形ABE,从而求解.
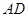 ∥
∥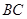 ,
,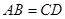 ,∴梯形
,∴梯形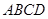 为等腰梯形,∴
为等腰梯形,∴ .
.又∵
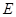 为
为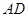 中点,∴
中点,∴ .
.在
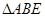 与
与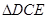 中,
中, , ∴
, ∴ …………(4分)
…………(4分)(2)∵
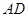 ∥
∥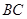 ,∴
,∴ .
.又∵
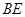 平分
平分 ,∴
,∴ ,
,∴
 ,∴
,∴ .
.又∵
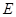 为
为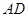 中点,
中点,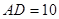 ,
,∴
 .………………………………(8分)
.………………………………(8分)(1)根据等腰梯形的性质可得∠BAE=∠CDE,再根据SAS即可证明;
(2)根据角平分线的定义和平行线的性质即可发现等腰三角形ABE,从而求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 是一张放在平面直角坐标系中的矩形纸片,点
是一张放在平面直角坐标系中的矩形纸片,点 在
在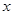 轴上,点
轴上,点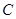 在
在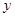 轴上,将边
轴上,将边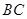 折叠,使点
折叠,使点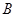 落在边
落在边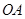 的点
的点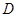 处.已知折叠
处.已知折叠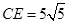 ,且
,且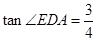 .
.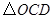 与
与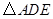 是否相似?请说明理由;
是否相似?请说明理由; 与
与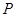 的坐标;
的坐标; ,使直线
,使直线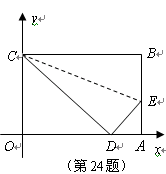
 中,
中, 是对角线.点
是对角线.点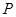 为矩形外一点且满足
为矩形外一点且满足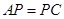 ,
,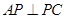 .
.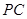 交
交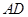 于点
于点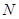 ,连接
,连接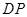 ,过点
,过点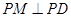 交
交 .
.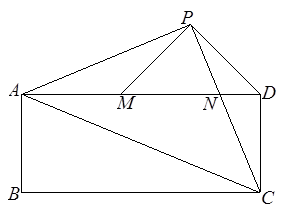
 ,求矩形
,求矩形 ,求证:
,求证: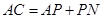 .
.
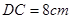 ,
, 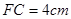 ,则
,则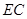 长为 ㎝.
长为 ㎝.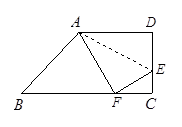
 ,有以下四个条件:①
,有以下四个条件:① ∥
∥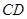 ;②
;②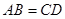 ;③
;③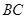 ∥
∥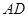 ;④
;④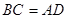 .从这四个条件中任选两个,能使四边形
.从这四个条件中任选两个,能使四边形