题目内容
2.△ABC是⊙O的内接三角形,⊙O的直径为10,∠ABC=45°,则AC的长是( )| A. | 5 | B. | 10 | C. | 5$\sqrt{2}$ | D. | 10$\sqrt{2}$ |
分析 如图,连接OA、OC.只要证明△OAC是等腰直角三角形即可解决问题.
解答 解:如图,连接OA、OC.
∵∠AOC=2∠ABC=90°,
∴△AOC的等腰直角三角形,
∴AC=$\sqrt{O{A}^{2}+O{C}^{2}}$=$\sqrt{{5}^{2}+{5}^{2}}$=5$\sqrt{2}$,
故选C.
点评 本题考查三角形的外接圆与外心、圆周角定理、勾股定理等知识,解题的关键是学会添加常用辅助线,构造特殊三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
10.下列实数中,是无理数是( )
| A. | $\frac{25}{3}$ | B. | 3.14 | C. | $\sqrt{5}$ | D. | $\root{3}{8}$ |
17. 如图,△ABC中,D为BC上的点,DC=2BD,以DC为直径作圆交AB于点E,若AE=AC,则sinB的值为( )
如图,△ABC中,D为BC上的点,DC=2BD,以DC为直径作圆交AB于点E,若AE=AC,则sinB的值为( )
 如图,△ABC中,D为BC上的点,DC=2BD,以DC为直径作圆交AB于点E,若AE=AC,则sinB的值为( )
如图,△ABC中,D为BC上的点,DC=2BD,以DC为直径作圆交AB于点E,若AE=AC,则sinB的值为( )| A. | $\frac{2}{5}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{\sqrt{10}}{8}$ | D. | $\frac{3\sqrt{6}}{8}$ |
7.若1<x<2,则|x-3|+$\sqrt{(x-1)^{2}}$的值为( )
| A. | 2x-4 | B. | 2 | C. | 4-2x | D. | -2 |
11.以下调查中,不适宜全面调查的是( )
| A. | 调查某班学生的身高情况 | |
| B. | 调查某批次灯泡的使用寿命 | |
| C. | 调查某舞蹈队成员的鞋码大小 | |
| D. | 调查班级某学习小组成员周末写作业的时间 |
12.用反证法证明“a<b”,应先假设( )
| A. | a≠b | B. | a>b | C. | a=b | D. | a≥b |
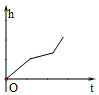
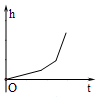
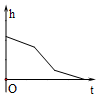
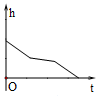
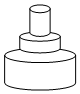 如图,匀速地向该容器内注水,最后把容器注满,在注水过程中容器内液面的高度h随时间t变化的函数图象最接近实际情况的是( )
如图,匀速地向该容器内注水,最后把容器注满,在注水过程中容器内液面的高度h随时间t变化的函数图象最接近实际情况的是( )