题目内容
如图,AB是⊙O 的直径,CD是⊙O的一条弦,且CD⊥AB于点E.
(1)求证:∠BCO=∠D;
(2)若CD= ,AE=2,求⊙O的半径.
,AE=2,求⊙O的半径.
∠BCO=∠D 半径=3.
解析试题分析:(1)证明:∵O为圆心,∴OB="OC," ∴∠BCO="∠B" 又∵∠B与∠D所对的同弧AC,∴∠B="∠D" ∴∠BCO=∠D (2)设半径为x,则EO="(x-2)," ∵CD⊥AB∴CE=DE=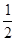 ×4
×4 =2
=2 在Rt△CEO中,由勾股定理得;CO2-OE2="CE2" 即x2-(x-2)2=(2
在Rt△CEO中,由勾股定理得;CO2-OE2="CE2" 即x2-(x-2)2=(2 )2 解得x="3" (1)证明:如图.
)2 解得x="3" (1)证明:如图.
∵OC=OB,
∴∠BCO=∠B.
∵∠B=∠D,
∴∠BCO=∠D. ………………………………2分
(2)解:∵AB是⊙O 的直径,且CD⊥AB于点E,
∴
 . ............................................ 3分
. ............................................ 3分
在Rt△OCE中, ,
,
设⊙O的半径为r,则OC=r,OE=OA AE=r
AE=r 2,
2,
∴ . ................................................... 4分
. ................................................... 4分
解得 .
.
∴⊙O 的半径为3. 5分
考点:垂径定理,勾股定理,在同圆等圆中圆周角与弧的关系。等腰三角形的性质。
点评:在同圆中,两个角要是相等的条件是所对的同一个弧,(1)中∴∠B=∠D,又∠B=∠BCO,∴等量代换证得。(2)中,根据勾股定理可列方程求之。中等偏难题,计算较多。

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
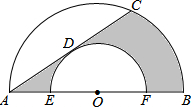 如图,AB是半圆O的直径,以O为圆心,OE长为半径的半圆交AB于E、F两点,弦AC是小半圆的切线,D为切点,已知AO=4,EO=2,那么阴影部分的面积是
如图,AB是半圆O的直径,以O为圆心,OE长为半径的半圆交AB于E、F两点,弦AC是小半圆的切线,D为切点,已知AO=4,EO=2,那么阴影部分的面积是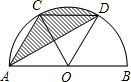 如图,AB是半⊙O的直径,C、D是半圆的三等分点,半圆的半径为4.阴影部分的面积为
如图,AB是半⊙O的直径,C、D是半圆的三等分点,半圆的半径为4.阴影部分的面积为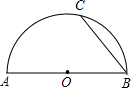 cm,点O到BC的距离为4cm.
cm,点O到BC的距离为4cm. (2013•惠城区模拟)如图,AB是半圆⊙O的直径,弦CD∥AB,∠CAD=30°,若AB=6,则阴影部分的面积是
(2013•惠城区模拟)如图,AB是半圆⊙O的直径,弦CD∥AB,∠CAD=30°,若AB=6,则阴影部分的面积是 如图,AB是半圆O的直径,∠BAC=60°,D是半圆上任意一点,那么∠D的度数是( )
如图,AB是半圆O的直径,∠BAC=60°,D是半圆上任意一点,那么∠D的度数是( )