题目内容
把数、理、化、语、英5本参考书,排成一行放在书架上,共有多少种不同的排法?
(1)文科、理科书交叉排放,共有多少种不同排法?
(2)两本文科书排在一起,共有多少种不同排法?
(3)化学不放在第1位,共有多少种不同排法?
(4)语文与数学必须相邻,共有多少种不同排法?
(5)物理与化学不得相邻,共有多少种不同排法?
(1)文科、理科书交叉排放,共有多少种不同排法?
(2)两本文科书排在一起,共有多少种不同排法?
(3)化学不放在第1位,共有多少种不同排法?
(4)语文与数学必须相邻,共有多少种不同排法?
(5)物理与化学不得相邻,共有多少种不同排法?
考点:计数方法
专题:
分析:(1)文科书与理科书交叉排放,理科书有3×2×1=6种可能,则文科书有2×1=2种可能,则共有6×2=12种不同排法.
(2)把两本文科书看作一个整体,有4×3×2×1=24种,两本文科书有2种顺序,故可得出总共的排列种类;
(3)由于化学不放在第1位,则第1位有4种可能,则共有4×4×3×2×1=96种不同排法;
(4)语文与数学必须相邻,有2×4=8种可能,则共有2×4×3×2×1=48种不同排法;
(5)物理与化学不得相邻,有5×4-2×4=12种可能,则共有12×3×2×1=72种不同排法;
(2)把两本文科书看作一个整体,有4×3×2×1=24种,两本文科书有2种顺序,故可得出总共的排列种类;
(3)由于化学不放在第1位,则第1位有4种可能,则共有4×4×3×2×1=96种不同排法;
(4)语文与数学必须相邻,有2×4=8种可能,则共有2×4×3×2×1=48种不同排法;
(5)物理与化学不得相邻,有5×4-2×4=12种可能,则共有12×3×2×1=72种不同排法;
解答:解:(1)3×2×1×2×1=12种.
故文科书与理科书交叉排放,共有12种不同排法.
(2)4×3×2×1×2=48种.
故两本文科书排在一起,共有48种不同排法;
(3)4×4×3×2×1=96种.
故化学不放在第1位,共有96种不同排法.
(4)2×4×3×2×1=48种.
故语文与数学必须相邻,共有48种不同排法.
(5)(5×4-2×4)×3×2×1=72种.
故物理与化学不得相邻,共有72种不同排法.
故文科书与理科书交叉排放,共有12种不同排法.
(2)4×3×2×1×2=48种.
故两本文科书排在一起,共有48种不同排法;
(3)4×4×3×2×1=96种.
故化学不放在第1位,共有96种不同排法.
(4)2×4×3×2×1=48种.
故语文与数学必须相邻,共有48种不同排法.
(5)(5×4-2×4)×3×2×1=72种.
故物理与化学不得相邻,共有72种不同排法.
点评:本题考查了乘法原理:完成一件工作共需n个步骤:完成第1个步骤有m1种方法,完成第2个步骤有m2种方法,…,完成第n个步骤有mn种方法,那么,完成这一件工作共有m1•m2•…•mn种方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列坐标表示的点中,不在反比例函数y=
的图象上的是( )
| 6 |
| x |
| A、(-2,-3) |
| B、(-1,-6) |
| C、(-0.5,12) |
| D、(1.5,4) |
 如图,在一张长方形纸片ABCD中,AB<AD,点E、F分别是AB和CD的中点,现将这张纸片按图示方式折叠,使点B落在线段EF上的点G处,折痕AK交EF于H,则下列说法正确的个数有( )
如图,在一张长方形纸片ABCD中,AB<AD,点E、F分别是AB和CD的中点,现将这张纸片按图示方式折叠,使点B落在线段EF上的点G处,折痕AK交EF于H,则下列说法正确的个数有( )①∠DAG=30°;②△GHK是正三角形;③GH=2EH;④FG=
| 3 |
| A、1个 | B、2个 | C、3个 | D、4个 |
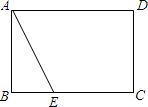 如图所示,在矩形ABCD中,∠BAE=
如图所示,在矩形ABCD中,∠BAE=| 1 |
| 2 |
| 3 |
A、
| ||||
| B、5 | ||||
C、
| ||||
D、2
|
 如图,在四边形ABCD中,∠ABC=∠ADC=90°,AC⊥BD于O,求证:AC平分∠BAD.
如图,在四边形ABCD中,∠ABC=∠ADC=90°,AC⊥BD于O,求证:AC平分∠BAD.
 如图,在⊙O中,直径AB⊥弦CD,垂足为P,OB=5,PB=2,求CD的长.
如图,在⊙O中,直径AB⊥弦CD,垂足为P,OB=5,PB=2,求CD的长.