题目内容
14.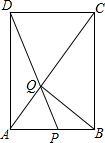 如图所示,在边长为4的正方形ABCD中,点P在AB上从A向B运动,连接DP交AC于点Q,
如图所示,在边长为4的正方形ABCD中,点P在AB上从A向B运动,连接DP交AC于点Q,(1)试证明:无论点P运动到AB上何处时,都有DQ=BQ;
(2)当点P在AB上运动到什么位置时,△ADQ的面积是正方形ABCD面积的$\frac{1}{6}$;
(3)若点P从点A运动到点B,再继续在BC上运动到点C,在整个过程中,当点P运动到什么位置时,△ADQ恰好为等腰三角形.
分析 1)根据正方形性质得出AB=AD,∠BAD=90°,∠DAC=∠BAC=45°,利用“边角边”证明△ADQ≌△ABQ即可得出结论;
(2)过点Q作QE⊥AD于E,QF⊥AB于F,则QE=QF=AE=AF,若△ADQ的面积是正方形ABCD面积的$\frac{1}{6}$,则有S△ADQ=$\frac{1}{2}$AD•QE=$\frac{1}{6}$S正方形ABCD,求得OE的值,再利用△DEQ∽△DAP有$\frac{QE}{AP}$=$\frac{DE}{DA}$解得AP值;
(3)点P运动时,△ADQ恰为等腰三角形的情况有三种:QD=QA或DA=DQ或AQ=AD.
①当点P运动到与点B重合时,QD=QA,此时△ADQ是等腰三角形;
②当点P与点C重合时,点Q与点C也重合,此时DA=DQ,△ADQ是等腰三角形;
③当AD=AQ=4时,有CP=CQ,CP=AC-AD而由正方形的对角线的性质得到CP的值.
解答 (1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,∠DAC=∠BAC=45°,
在△ADQ和△ABQ中,
$\left\{\begin{array}{l}{AB=AD}\\{∠DAC=BAC}\\{AQ=AQ}\end{array}\right.$,
∴△ADQ≌△ABQ(SAS),
∴DQ=BQ;
(2)解:△ADQ的面积恰好是正方形ABCD面积的$\frac{1}{6}$时,
过点Q作QE⊥AD于E,QF⊥AB于F,如图1所示:
则四边形AFQE为正方形,
∴QE=QF=AE=AF,
∵在边长为4的正方形ABCD中,
∴S正方形ABCD=16,
∴$\frac{1}{2}$AD×QE=$\frac{1}{6}$S正方形ABCD=$\frac{1}{6}$×16=$\frac{8}{3}$,
∴QE=$\frac{4}{3}$,
∵EQ∥AP,
∴△DEQ∽△DAP,
∴$\frac{QE}{AP}$=$\frac{DE}{DA}$,即$\frac{\frac{4}{3}}{AP}=\frac{4-\frac{3}{4}}{4}$,
解得AP=2,
∴AP=2时,△ADQ的面积是正方形ABCD面积的$\frac{1}{6}$;
(3)解:如图2所示:
若△ADQ是等腰三角形,则有QD=QA或DA=DQ或AQ=AD,
①当AD=DQ时,则∠DQA=∠DAQ=45°
∴∠ADQ=90°,P为C点,
②当AQ=DQ时,则∠DAQ=∠ADQ=45°,
∴∠AQD=90°,P为B,
③AD=AQ(P在BC上),
∴CQ=AC-AQ=$\sqrt{2}$BC-BC=($\sqrt{2}$-1)BC
∵AD∥BC,
∴△ADQ∽△CQP,
∴$\frac{CP}{AD}$=$\frac{CQ}{AQ}$,即可得$\frac{CP}{CQ}$=$\frac{AD}{AQ}$=1,
∴CP=CQ=($\sqrt{2}$-1)BC=4($\sqrt{2}$-1)
综上所述:P在B点,C点,或在CP=4($\sqrt{2}$-1)处,△ADQ是等腰三角形.
点评 本题是四边形综合题目,考查了正方形的性质、全等三角形的判定与性质、相似三角形的判定与性质、三角形的面积公式、等腰三角形的性质、等腰直角三角形的性质等知识;本题综合性强,难度较大,(3)需要分类讨论.

| A. | -3.14是负数,不是分数 | |
| B. | 有理数不是负数就是正数 | |
| C. | 没有最大的负整数 | |
| D. | -2000既是负数,也是整数,还是有理数 |
| A. | a-1<b-1 | B. | $\frac{a}{3}$<$\frac{b}{3}$ | C. | -a>-b | D. | ac<bc |
| A. | 2.175×108元 | B. | 2.175×107 元 | C. | 2.175×109 元 | D. | 2.175×106元 |