题目内容
5.小华和小明同时从环形跑道上一点向相反方向走去,小华每分钟走65米,小明每分钟走75米,经过2.5分钟相遇.(1)按照同样的速度与行走方式,在经过5分钟,两人第二次相遇;
(2)若两人同时从环形跑道上的一点向相同方向走去,速度不变,经过多长时间,两人第二次相遇.
分析 (1)设按照同样的速度与行走方式,在经过 x分钟,两人第二次相遇.第二次相遇时,两人一共走了2圈;
(2)根据两人长跑的过程中当第二次两人相遇时路程的差为700米列出方程求解即可.
解答 解:(1)设按照同样的速度与行走方式,在经过 x分钟,两人第二次相遇,则
(65+75)x=2×2.5×(65+75),
解得x=5.
故答案是:5;
(2)设两人从同一地点同时同向起跑,经过y 分钟两人第二次相遇,根据题意得:
75y-65y=2×2.5×(65+75),
解得:y=70.
答:两人从同一地点同时同向起跑,70分钟后两人第二次相遇.
点评 本题考查了一元一次方程的应用,记住有关追击问题中的等量关系是解决本题的关键.

练习册系列答案
相关题目
16. 今年我国中东部大部分地区持续出现雾霾天气.某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了尚不完整的统计图表.
今年我国中东部大部分地区持续出现雾霾天气.某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了尚不完整的统计图表.
请根据图表中提供的信息解答下列问题:
(1)填空:m=40,n=100,扇形统计图中E组所占的百分比为15%;
(2)若该市人口约有100万人,请你估计其中持D组“观点”的市民人数.
 今年我国中东部大部分地区持续出现雾霾天气.某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了尚不完整的统计图表.
今年我国中东部大部分地区持续出现雾霾天气.某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了尚不完整的统计图表.| 级别 | 观 点 | 频数(人数) |
| A | 大气气压低,空气不流动 | 80 |
| B | 地面灰尘大,空气湿度低 | m |
| C | 汽车尾气捧放 | n |
| D | 工厂造成的污染 | 120 |
| E | 其他 | 60 |
(1)填空:m=40,n=100,扇形统计图中E组所占的百分比为15%;
(2)若该市人口约有100万人,请你估计其中持D组“观点”的市民人数.
20.从标号分别为1,2,3,4,5的5张卡片中,随机抽取1张,下列事件中,必然事件是( )
| A. | 该卡片标号不大于5 | B. | 该卡片标号大于5 | ||
| C. | 该卡片标号是奇数 | D. | 该卡片标号是3 |
10.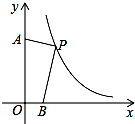 已知P是反比例函数y=$\frac{12}{x}$(x>0)图象上一点,点B的坐标为(5,0),A是y轴正半轴上一点,且AP⊥BP,AP:BP=1:3,那么四边形AOBP的面积为( )
已知P是反比例函数y=$\frac{12}{x}$(x>0)图象上一点,点B的坐标为(5,0),A是y轴正半轴上一点,且AP⊥BP,AP:BP=1:3,那么四边形AOBP的面积为( )
 已知P是反比例函数y=$\frac{12}{x}$(x>0)图象上一点,点B的坐标为(5,0),A是y轴正半轴上一点,且AP⊥BP,AP:BP=1:3,那么四边形AOBP的面积为( )
已知P是反比例函数y=$\frac{12}{x}$(x>0)图象上一点,点B的坐标为(5,0),A是y轴正半轴上一点,且AP⊥BP,AP:BP=1:3,那么四边形AOBP的面积为( )| A. | 16 | B. | 20 | C. | 24 | D. | 28 |
17.下列各数中,最大的数是( )
| A. | |-3| | B. | -2 | C. | 0 | D. | 1 |
14.下列计算正确的是( )
| A. | 2a-a=2 | B. | (a-1)2=a2-1 | C. | (-4a6)÷(-2a2)=2a4 | D. | a2•a4=a8 |
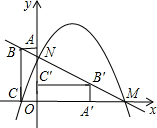 如图,平面直角坐标系中,矩形OABC的顶点A(0,3),C(-1,0).将矩形OABC绕原点顺时针旋转90°,得到矩形OA′B′C′.解答下列问题:
如图,平面直角坐标系中,矩形OABC的顶点A(0,3),C(-1,0).将矩形OABC绕原点顺时针旋转90°,得到矩形OA′B′C′.解答下列问题: