Question

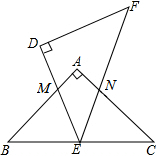如图，△ABC和△DEF是两个等腰直角三角形，∠A=∠D=90°，△DEF的顶点E位于边BC的中点上．设DE与AB交于M，EF与AC交于点N，求证：△BEM∽△CNE．

Answer 1

考点：相似三角形的判定

专题：证明题

分析：由△ABC和△DEF是两个等腰直角三角形，∠A=∠D=90°，易得∠2=∠4，又由∠B=∠C=45°，即可证得△BEM∽△CNE．

解答：证明：∵△ABC是等腰直角三角形，
∴∠B=45°，
∴∠1+∠2=135°
又∵△DEF是等腰直角三角形，
∴∠3=45°
∴∠1+∠4=135°
∴∠2=∠4，
∵∠B=∠C=45°，
∴△BEM∽△CNE．

点评：此题考查了相似三角形的判定与性质以及等腰直角三角形性质．此题难度适中，注意掌握数形结合思想的应用．