题目内容
5．
如图所示，1条直线将平面分成2个部分，2条直线最多可将平面分成4个部分，3条直线最多可将平面分成7个部分，4条直线最多可将平面分成11个部分．现有n条直线最多可将平面分成56个部分，则n的值为10．
分析 n条直线最多可将平面分成S=1+1+2+3…+n=$\frac{1}{2}$n（n+1）+1，依此可得等量关系：n条直线最多可将平面分成56个部分，列出方程求解即可．
解答 解：依题意有
$\frac{1}{2}$n（n+1）+1=56，
解得n1=-11（不合题意舍去），n2=10．
答：n的值为10．
故答案为：10．
点评 考查了点、线、面、体，规律性问题及一元二次方程的应用；得到分成的最多平面数的规律是解决本题的难点．
练习册系列答案
发散思维新课堂系列答案
相关题目
如图，矩形ABCD是供一辆机动车停放的车位示意图，已知BC=2m，CD=5.4m，∠DCF=30°，请你计算车位所占的宽度EF约为多少米．（结果精确到0.1m，$\sqrt{3}$≈1.73）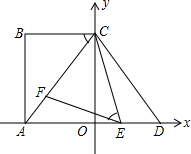
如图：在平面直角坐标系中，点A、C分别在x轴负半轴、y轴正半轴上，且四边形ABCD为矩形，AB=4，点D与点A关于原点O成中心对称，tan∠ACB=$\frac{4}{3}$，点E、F分别是线段AD、AC上的动点（点E不与点A、D重合），且∠CEF=∠ACB．
在△ABC中，AB=15，BC=14，AC=13，求△ABC的面积．
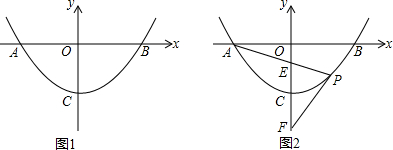
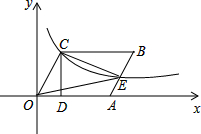已知四边形OABC是菱形，CD⊥x轴，垂足为D，函数$y=\frac{8}{x}$的图象经过点C，且与AB交于点E，若OD=2，则△OCE的面积为4$\sqrt{5}$．
如图，在平面直角坐标系中，OA⊥OB，AB⊥x轴于点C，点A（$\sqrt{3}$，1）在反比例函数y=$\frac{k}{x}$的图象上．