题目内容
一块直角三角形木板的一条直角边长1.5米,面积为1.5平方米,要把它加工成一个面积最大的正方形桌面,问:怎样加工面积最大?
考点:相似三角形的应用,二次函数的最值
专题:
分析:首先利用面积和一条直角边的长求得另一条直角边的长,然后分两个方案求解后得到面积最大的方案即可;
方案一:根据题意画出图形,作CM⊥AB于M,交DE于N.设正方形边长为xcm,再根据直角三角形的面积得出CM的长,利用相似三角形的判定定理即可得出△CDE∽△CAB,再根据相似三角形的对应边成比例即可求出正方形的边长;
方案二:如图(2)设正方形边长为ycm,利用相似三角形的判定定理即可得出△BFE∽△BCA,再根据相似三角形的对应边成比例即可求出正方形的边长;把两方案中正方形的边长进行比较即可得出结论.
方案一:根据题意画出图形,作CM⊥AB于M,交DE于N.设正方形边长为xcm,再根据直角三角形的面积得出CM的长,利用相似三角形的判定定理即可得出△CDE∽△CAB,再根据相似三角形的对应边成比例即可求出正方形的边长;
方案二:如图(2)设正方形边长为ycm,利用相似三角形的判定定理即可得出△BFE∽△BCA,再根据相似三角形的对应边成比例即可求出正方形的边长;把两方案中正方形的边长进行比较即可得出结论.
解答: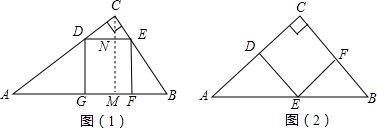 解:∵一条直角边长1.5米,面积为1.5平方米,
解:∵一条直角边长1.5米,面积为1.5平方米,
∴另一条直角边的长为2米,
方案一:如图(1),
作CM⊥AB于M,交DE于N.
设正方形边长为xcm.
由S△ABC=
AC•BC=
AB•CM
知:CM=
=
∵DE∥AB
∴△CDE∽△CAB,
即:
=
∴
=
∴x=
方案二:如图(2)设正方形边长为ycm.
∵EF∥AC
∴△BFE∽△BCA,
∴
=
即
=
∴y=
∵x<y,
∴方案二裁出的正方形的面积最大.
这时正方形的边长是
cm.
 解:∵一条直角边长1.5米,面积为1.5平方米,
解:∵一条直角边长1.5米,面积为1.5平方米,∴另一条直角边的长为2米,
方案一:如图(1),
作CM⊥AB于M,交DE于N.
设正方形边长为xcm.
由S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
知:CM=
| AC•BC |
| AB |
| 6 |
| 5 |
∵DE∥AB
∴△CDE∽△CAB,
即:
| CN |
| CM |
| DE |
| AB |
∴
| ||
|
| x |
| 2.5 |
∴x=
| 30 |
| 37 |
方案二:如图(2)设正方形边长为ycm.
∵EF∥AC
∴△BFE∽△BCA,
∴
| BF |
| BC |
| EF |
| AC |
即
| 1.5-y |
| 1.5 |
| y |
| 2 |
∴y=
| 6 |
| 7 |
∵x<y,
∴方案二裁出的正方形的面积最大.
这时正方形的边长是
| 6 |
| 7 |
点评:本题考查的是相似三角形在实际生活中的应用,能根据题意画出图形,作出辅助线,再根据相似三角形的判定定理及性质进行解答即可.

练习册系列答案
相关题目
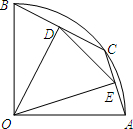 如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合),OD⊥BC,OE⊥AC,垂足分别为D、E,则线段DE的长为( )
如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合),OD⊥BC,OE⊥AC,垂足分别为D、E,则线段DE的长为( ) 在如图方格纸中平移四边形ABCD,使点A移到点A′,使点B移到点B′,使点C移到点C′,使点D移到点D′,画出平移后的四边形A′B′C′D′.
在如图方格纸中平移四边形ABCD,使点A移到点A′,使点B移到点B′,使点C移到点C′,使点D移到点D′,画出平移后的四边形A′B′C′D′.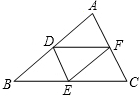 如图,在△ABC中,点D、E、F分别是AB、BC、CA的中点,求证:△ABC∽△DEF.
如图,在△ABC中,点D、E、F分别是AB、BC、CA的中点,求证:△ABC∽△DEF.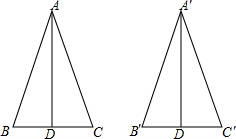 如图,AD、A′D′分别是△ABC和△A′B′C′的边BC、B′C′上的高,且AD=A′D′,AB=A′B′,∠BAC=∠B′A′C′.
如图,AD、A′D′分别是△ABC和△A′B′C′的边BC、B′C′上的高,且AD=A′D′,AB=A′B′,∠BAC=∠B′A′C′. 如图,在平整的地面上,有若干个完全相同的棱长为10cm的小正方体堆成一个几何体.
如图,在平整的地面上,有若干个完全相同的棱长为10cm的小正方体堆成一个几何体. 如图,两条直线a,b相交.
如图,两条直线a,b相交.