Question

观察控究，完成证明和填空．

如图，四边形ABCD中，点E、F、G、H分别是边AB、BC、CD、DA的中点，顺次连接E、F、G、H，得到的四边形EFGH叫中点四边形．

（1）求证：四边形EFGH是平行四边形；

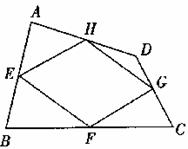
（2）如图，当四边形ABCD变成等腰梯形时，它的中点四边形是菱形，请你探究并填空：

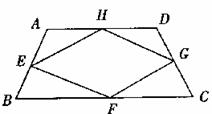
当四边形ABCD变成平行四边形时，它的中点四边形是＿＿＿＿＿＿＿＿＿＿；

当四边形ABCD变成矩形时，它的中点四边形是＿＿＿＿＿＿＿＿＿＿；

当四边形ABCD变成菱形时，它的中点四边形是＿＿＿＿＿＿＿＿＿＿；

当四边形ABCD变成正方形时，它的中点四边形是＿＿＿＿＿＿＿＿＿＿；

（3）根据以上观察探究，请你总结中点四边形的形状由原四边形的什么决定的？

Answer 1

（1）证明：连接BD

    ∵E、H分别是AB、AD的中点，

∴EH是△ABD的中位线

∴EH＝BD，EH∥BD         

同理得FG＝BD，FG∥BD

∴EH＝FG，EH∥FG            

∴四边形EFGH是平行四边形         

（2）填空依次为平行四边形，菱形，矩形，正方形   

（3）中点四边形的形状由原四边形的对角线的关系来决定的．