题目内容
如图1,在菱形ABCD中,∠A=60°.点E,F分别是边AB,AD上的点,且满足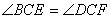 ,连结EF.
,连结EF.
(1)若AF=1,求EF的长;
(2)取CE的中点M,连结BM,FM,BF.求证: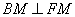 ;
;
(
|

 ,
,
 若
若 点E,F
点E,F 分别是边AB,AD延长线上的点,其它条件不变,结论
分别是边AB,AD延长线上的点,其它条件不变,结论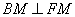 是否仍然成立(不需证明).
是否仍然成立(不需证明). 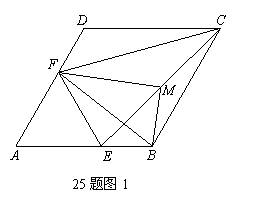
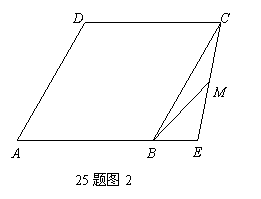
(1)解:∵四边形ABCD是菱形,
∴ AB = AD = BC= DC,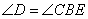 .
.
又∵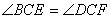 ,
,
∴△CBE≌△CDF.
∴BE=DF.
又∵AB =AD,∴AB-BE =AD-DF,即AE=AF.
又∵∠A=60°,∴△AEF是等边三角形.
∴EF=AF.
∵AF=1,∴EF=1.
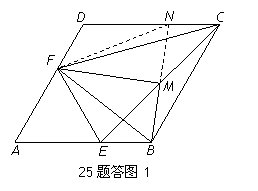
(2)证明:延长BM交DC于点N,连结FN.(如答图)
∵四边形ABCD是菱形,
∴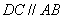 ,
,
∴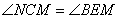 ,
, .
.
∵点M是CE的中点,
∴CM=EM.
∴△CMN≌△EMB.
∴NM=MB,CN=BE.
又∵AB = DC.∴DC-CN=AB-BE, 即DN=AE.
∵ 是等边三角形,∴
是等边三角形,∴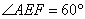 ,EF=AE.
,EF=AE.
 ∴
∴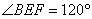 ,EF=DN.
,EF=DN.
∵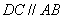 ,∴
,∴ .
.
又∵∠A=60°,∴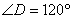 ,
,
∴ .
.
又∵DN=EF,BE=DF.
∴△FDN≌△BEF.
∴FN=FB,
又∵NM=MB,∴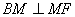 .
.
(3)结论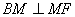 仍然成立
仍然成立

练习册系列答案
相关题目

 的两个实数根中较大的根是 .
的两个实数根中较大的根是 . 中,点E,F是对角线AC上的两点,且AE=CF,连结BE,DF.
中,点E,F是对角线AC上的两点,且AE=CF,连结BE,DF.
 +1)(
+1)(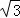 ﹣1)2+(
﹣1)2+(