题目内容
15.如果$\frac{{a}^{-1}+b}{a+{b}^{-1}}$=k,则$\frac{{a}^{-2}+{b}^{2}}{{a}^{2}+{b}^{-2}}$等于k2.分析 首先由$\frac{{a}^{-1}+b}{a+{b}^{-1}}$=k,根据负整数指数幂的意义及分式的基本性质得出$\frac{b}{a}$=k,再化简$\frac{{a}^{-2}+{b}^{2}}{{a}^{2}+{b}^{-2}}$=$\frac{{b}^{2}}{{a}^{2}}$=($\frac{b}{a}$)2=k2.
解答 解:∵$\frac{{a}^{-1}+b}{a+{b}^{-1}}$=$\frac{\frac{1}{a}+b}{a+\frac{1}{b}}$=$\frac{b+a{b}^{2}}{{a}^{2}b+a}$=$\frac{b}{a}$=k,
∴$\frac{{a}^{-2}+{b}^{2}}{{a}^{2}+{b}^{-2}}$=$\frac{{b}^{2}+{a}^{2}{b}^{4}}{{a}^{4}{b}^{2}+{a}^{2}}$=$\frac{{b}^{2}}{{a}^{2}}$=($\frac{b}{a}$)2=k2.
故答案为k2.
点评 此题考查了负整数指数幂的意义:a-p=$\frac{1}{{a}^{p}}$(a≠0,p为正整数),正确化简分式,得出$\frac{{a}^{-1}+b}{a+{b}^{-1}}$=$\frac{b}{a}$是解题关键.

练习册系列答案
相关题目
5.2014年五一“黄金周”全市接待游客总数为996000人次.将数996000用科学记数法表示应为( )
| A. | 0.996×106 | B. | 96.6×105 | C. | 9.96×105 | D. | 9.96×104 |
 如图,弦AB与⊙O相交于A、B两点,已知⊙O的直径为10,若圆心O到AB的距离为3,那么弦AB长为8.
如图,弦AB与⊙O相交于A、B两点,已知⊙O的直径为10,若圆心O到AB的距离为3,那么弦AB长为8.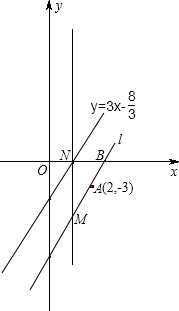 如图,在平面直角坐标系中,直线l经过点A(2,-3),与x轴交于点B,且与直线$y=3x-\frac{8}{3}$平行.
如图,在平面直角坐标系中,直线l经过点A(2,-3),与x轴交于点B,且与直线$y=3x-\frac{8}{3}$平行.