Question

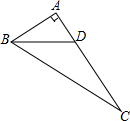
如图所示，在Rt△ABC中，AB=AC，∠BAC=90°，D为BC的中点。
（1）写出点D到△ABC三个顶点A、B、C的距离的关系（不要求说明为什么）；
（2）如果点M、N分别在线段AB、AC上移动，在移动中保持AN=BM，请判断△DMN的形状，并说明理由。

Answer 1

（1）AD=BD=CD；
（2）△DMN是等腰直角三角形。
理由：连结AD，则AD=BD，∠CAD=45°，∠B=45°，
在△AND和△BMD中，，
所以△AND≌△BMD，
所以ND=MD，∠NDA=∠MDB，
又∠MDB+∠MDA=90°，所以∠NDA+∠MDA=∠MDN=90°。
在△DMN中，ND=MD，∠MDN=90°，所以△DMN是等腰直角三角形。