题目内容
6.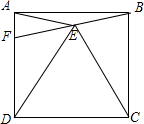 如图,E是正方形ABCD内一点,△CDE是等边三角形,连接EB、EA,延长BE交AD边于点F.则∠AFB的度数是( )
如图,E是正方形ABCD内一点,△CDE是等边三角形,连接EB、EA,延长BE交AD边于点F.则∠AFB的度数是( )| A. | 45° | B. | 60° | C. | 80° | D. | 75° |
分析 先由正方形和等边三角形的性质求出BC=CE,∠BCE=30°,再求出∠CBE,即可得出∠AFB.
解答 解:∵四边形ABCD是正方形,△CDE是等边三角形,
∴BC=CD,∠DAB=∠ABC=∠BCD=90°,CD=CE,∠DCE=60°,
∴BC=CE,∠BCE=90°-60°=30°,
∴∠CBE=$\frac{1}{2}$(180°-30°)=75°,
∴∠ABF=90°-75°=15°,
∴∠AFB=90°-15°=75°;
故选:D.
点评 本题考查了正方形的性质、等边三角形的性质以及等腰三角形的判定与性质;弄清各个角之间的关系是解决问题的关键.

练习册系列答案
相关题目
1.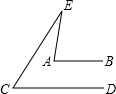 如图所示,已知AB∥CD,∠E=28°,∠C=52°,则∠EAB的度数是( )
如图所示,已知AB∥CD,∠E=28°,∠C=52°,则∠EAB的度数是( )
 如图所示,已知AB∥CD,∠E=28°,∠C=52°,则∠EAB的度数是( )
如图所示,已知AB∥CD,∠E=28°,∠C=52°,则∠EAB的度数是( )| A. | 28° | B. | 52° | C. | 80° | D. | 70° |
15. 如图,在?ABCD中,点E、F分别在AB、CD上,且AE=CF,则四边形BFDE不可能是( )
如图,在?ABCD中,点E、F分别在AB、CD上,且AE=CF,则四边形BFDE不可能是( )
 如图,在?ABCD中,点E、F分别在AB、CD上,且AE=CF,则四边形BFDE不可能是( )
如图,在?ABCD中,点E、F分别在AB、CD上,且AE=CF,则四边形BFDE不可能是( )| A. | 矩形 | B. | 菱形 | C. | 梯形 | D. | 平行四边形 |
16.已知x=3是方程x2-2x+a=0的根,则a等于( )
| A. | 1 | B. | -1 | C. | 3 | D. | -3 |
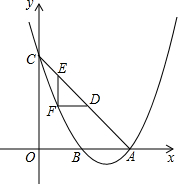 如图,当x=2时,抛物线y=ax2+bx+c取得最小值-1,并且抛物线与y轴交于点C(0,3),与x轴交于点A、B.
如图,当x=2时,抛物线y=ax2+bx+c取得最小值-1,并且抛物线与y轴交于点C(0,3),与x轴交于点A、B.