Question

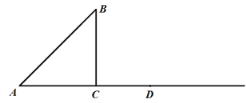
【题目】如图，己知，，，斜边，为垂直平分线，且，连接，.

（1）直接写出__________，__________；

（2）求证：是等边三角形；

（3）如图，连接，作，垂足为点，直接写出的长；

（4）是直线上的一点，且，连接，直接写出的长.

Answer 1

【答案】（1），（2）证明见解析（3）（4）或

【解析】

（1）根据含有30°角的直角三角形的性质可得BC=2，再由勾股定理即可求出AC的长；

（2）由为垂直平分线可得DB=DA，在Rt△BDE中，由勾股定理可得BD=4，可得BD=2BE，故∠BDE为60°，即可证明是等边三角形；

（3）由（1）（2）可知，，AD=4，进而可求得CD的长，再由等积法可得，代入求解即可；

（4）分点P在线段AC上和AC的延长线上两种情况，过点E作AC的垂线交AC于点Q，构造Rt△PQE，再根据勾股定理即可求解.

（1）∵，，，斜边，

∴，∴；

（2）∵为垂直平分线，∴ADB=DA，

在Rt△BDE中，

∵，，

∴，

∴BD=2BE，∴∠BDE为60°，

∴为等边三角形；

（3））由（1）（2）可知，，AD=4，

∴，

∵，

∴，

∴；

（4）分点P在线段AC上和AC的延长线上两种情况，

如图，过点E作AC的垂线交AC于点Q，

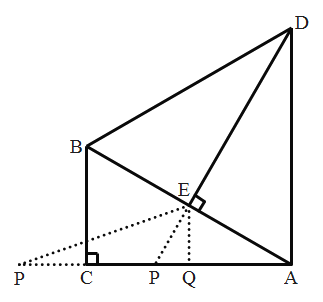
∵AE=2，∠BAC=30°，∴EQ=1，

∵，∴，

①若点P在线段AC上，

则，

∴；

②若点P在线段AC的延长线上，

则，

∴；

综上，PE的长为或.