题目内容
1.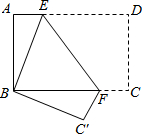 如图所示,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠EFC′=120°,那么∠ABE的度数为( )
如图所示,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠EFC′=120°,那么∠ABE的度数为( )| A. | 15° | B. | 25° | C. | 20° | D. | 30° |
分析 由折叠的性质知:∠EBC′、∠BC′F都是直角,∠BEF=∠DEF,因此BE∥C′F,那么∠EFC′和∠BEF互补,这样可得出∠BEF的度数,进而可求得∠AEB的度数,则∠ABE可在Rt△ABE中求得.
解答 解:由折叠的性质知,∠BEF=∠DEF,∠EBC′、∠BC′F都是直角,
∴BE∥C′F,
∴∠EFC′+∠BEF=180°,
又∵∠EFC′=120°,
∴∠BEF=∠DEF=60°,
在Rt△ABE中,可求得∠ABE=90°-∠AEB=30°.
故选D.
点评 本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
11.有下列命题:①若a>b,则a-b>0;②若a>b>c>0,则ac>bc;③若$\frac{a}{2}$-3>$\frac{b}{2}$-3,则a<b;④若a<b<0,则$\frac{a}{b}$>1.其中真命题有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.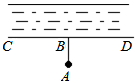 如图,计划把河水引到水池A中,先作AB⊥CD,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的数学根据是( )
如图,计划把河水引到水池A中,先作AB⊥CD,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的数学根据是( )
 如图,计划把河水引到水池A中,先作AB⊥CD,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的数学根据是( )
如图,计划把河水引到水池A中,先作AB⊥CD,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的数学根据是( )| A. | 两点之间,线段最短 | |
| B. | 两条平行线之间的距离处处相等 | |
| C. | 经过直线上或直线外一点,有且只有一条直线与已知直线垂直 | |
| D. | 直线外一点与直线上各点连接的所有线段中,垂线段最短 |
16.下列代数式中是分式的为( )
| A. | $\frac{x}{x+2}$ | B. | $\frac{{x}^{2}-2}{π}$ | C. | $\frac{4x}{7}$ | D. | $\frac{3-x}{4}$ |
6.以下列各组长度的线段为边,能构成三角形的是( )
| A. | 8,4,4 | B. | 5,6,12 | C. | 6,8,10 | D. | 1,2,3 |
10.在菱形ABCD中,若AB=2,则菱形的周长为( )
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
11. 如图,被笑脸盖住的点的坐标可能是( )
如图,被笑脸盖住的点的坐标可能是( )
 如图,被笑脸盖住的点的坐标可能是( )
如图,被笑脸盖住的点的坐标可能是( )| A. | (5,2) | B. | (-5,2) | C. | (-5,-2) | D. | (5,-2) |
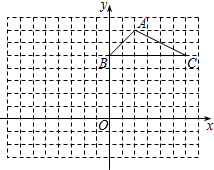 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系,
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系,