题目内容
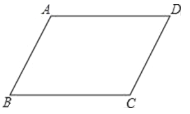
【题目】已知:PA=![]() ,PB=4,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.
,PB=4,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.
(1)如图,当∠APB=45°时,求AB及PD的长;
(2)当∠APB变化,且其它条件不变时,求PD的最大值,及相应∠APB的大小.
【答案】
【1】(1)①如图11,作AE⊥PB于点E.
∵△APE中,∠APE=45°,![]() ,
,
∴![]() ,
,
![]() .
.
∵![]() ,
,
∴![]() .
.
在Rt△ABE中,∠AEB=90°,
∴![]() .…………1分
.…………1分
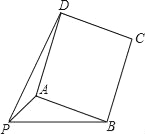
②解法一:如图12,因为四边形ABCD为正方形,可将
△PAD绕点A顺时针旋转90°得到△![]() ,
,
可得△![]() ≌△
≌△![]() ,
,![]() ,
,![]() .
.
∴![]() =90°,
=90°,![]() =45°,
=45°,![]() =90°.
=90°.
∴![]() .分
.分
∴![]() .…………2分
.…………2分
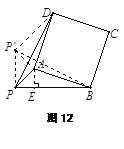
 解法二:如图13,过点P作AB的平行线,与DA的延长线交于F,设DA的 延长线交PB于G.
解法二:如图13,过点P作AB的平行线,与DA的延长线交于F,设DA的 延长线交PB于G.
在Rt△AEG中,可得
![]() ,
,
![]() ,
,![]() .
.
在Rt△PFG中,可得![]() ,
,![]() .
.
在Rt△PDF中,可得![]()
![]() .
.
【2】(2)如图14所示,将△PAD绕点A顺时针旋转90°得到△![]() , PD 的最大值即为
, PD 的最大值即为![]() 的最大值.
的最大值.
∵△![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
且P、D两点落在直线AB的两侧,
∴当![]() 三点共线时,
三点共线时,![]() 取得最大值(见图15).
取得最大值(见图15).
此时![]() ,即
,即![]() 的最大值为6. …………4分
的最大值为6. …………4分
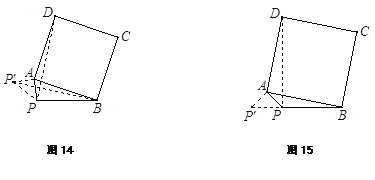 此时∠APB=180°-
此时∠APB=180°-![]() =135°. …………5分
=135°. …………5分
【解析】
(1)作辅助线,过点A作AE⊥PB于点E,在Rt△PAE中,已知∠APE,AP的值,根据三角函数可将AE,PE的值求出,由PB的值,可求BE的值,在Rt△ABE中,根据勾股定理可将AB的值求出;
求PD的值有两种解法,解法一:可将△PAD绕点A顺时针旋转90°得到△P'AB,可得△PAD≌△P'AB,求PD长即为求P′B的长,在Rt△AP′P中,可将PP′的值求出,在Rt△PP′B中,根据勾股定理可将P′B的值求出;
解法二:过点P作AB的平行线,与DA的延长线交于F,交PB于G,在Rt△AEG中,可求出AG,EG的长,进而可知PG的值,在Rt△PFG中,可求出PF,在Rt△PDF中,根据勾股定理可将PD的值求出;
(2)将△PAD绕点A顺时针旋转90°,得到△P'AB,PD的最大值即为P'B的最大值,故当P'、P、B三点共线时,P'B取得最大值,根据P'B=PP'+PB可求P'B的最大值,此时∠APB=180°-∠APP'=135°.
(1)①
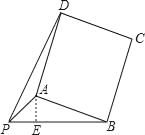
如图,作AE⊥PB于点E,
∵△APE中,∠APE=45°,PA=![]() ,
,
∴AE/span>=PE=![]() ×
×![]() =1,
=1,
∵PB=4,∴BE=PB﹣PE=3,
在Rt△ABE中,∠AEB=90°,
∴AB=![]() =
=![]() .
.
②解法一:
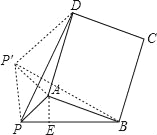
如图,因为四边形ABCD为正方形,可将
△PAD绕点A顺时针旋转90°得到△P'AB,
可得△PAD≌△P'AB,PD=P'B,PA=P'A.
∴∠PAP'=90°,∠APP'=45°,∠P'PB=90°
∴PP′=![]() PA=2,
PA=2,
∴PD=P′B=![]() =
=![]() =
=![]() ;
;
解法二:
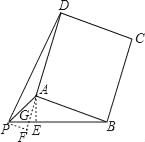
如图,过点P作AB的平行线,与DA的延长线交于F,与DA的
延长线交PB于G.
在Rt△AEG中,
可得AG=![]() =
=![]() =
=![]() ,EG=
,EG=![]() ,PG=PE﹣EG=
,PG=PE﹣EG=![]() .
.
在Rt△PFG中,
可得PF=PGcos∠FPG=PGcos∠ABE=![]() ,FG=
,FG=![]() .
.
在Rt△PDF中,可得,
PD=![]() =
=![]() =
=![]() .
.
(2)如图所示,

将△PAD绕点A顺时针旋转90°
得到△P'AB,PD的最大值即为P'B的最大值,
∵△P'PB中,P'B<PP'+PB,PP′=![]() PA=2,PB=4,
PA=2,PB=4,
且P、D两点落在直线AB的两侧,
∴当P'、P、B三点共线时,P'B取得最大值(如图)
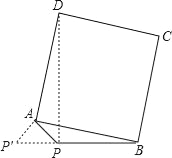
此时P'B=PP'+PB=6,即P'B的最大值为6.
此时∠APB=180°﹣∠APP'=135度.
考查综合应用解直角三角形、直角三角形性质,进行逻辑推理能力和运算能力,在解题过程中通过添加辅助线,确定P′B取得最大值时点P′的位置.

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案