题目内容
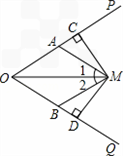
28、如图，M为∠POQ内一点，MA=MB，∠1=∠2，MC⊥OP于C，MD⊥OQ于D．求证：MC=MD．分析：首先利用SAS证明△AMO≌△BMO，得∠AOM=∠BOM，然后根据角平分线的性质得出MC=MD．
解答：证明：∵MA=MB，∠1=∠2，
又∵OM=OM，
∴△AMO≌△BMO（SAS）．
∴∠AOM=∠BOM．
又∵MC⊥OP于C，MD⊥OQ于D，
∴MC=MD．
又∵OM=OM，
∴△AMO≌△BMO（SAS）．
∴∠AOM=∠BOM．
又∵MC⊥OP于C，MD⊥OQ于D，
∴MC=MD．
点评：本题考查了全等三角形的判定、全等三角形的性质、角平分线的性质等知识，证出∠AOM=∠BOM是正确解决本题的关键．
练习册系列答案
相关题目
如图，在第一象限内作射线OC，与x轴的夹角为30°，在射线OC上取一点A，过点A作AH⊥x轴于点H，得到△AOH．在抛物线y=x2（x＞0）上取点P，在y轴上取点Q，使得以P，O，Q为顶点的三角形△POQ与△AOH全等，则符合条件的△AOH的面积是
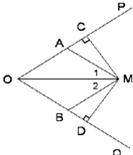
如图，M为∠POQ内一点，MA=MB，∠1=∠2，MC⊥OP于C，MD⊥OQ于D．求证：MC=MD．