题目内容
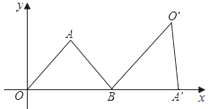
【题目】如图,将![]() 绕着点B顺时针旋转至
绕着点B顺时针旋转至![]() ,使得C点落在AB的延长线上的D点处,
,使得C点落在AB的延长线上的D点处,![]() 的边BC恰好是
的边BC恰好是![]() 的角平分线.
的角平分线.
(1)试求旋转角![]() 的度数;
的度数;
(2)设BE与AC的交点为点P,求证:![]() .
.

【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)根据旋转的性质,得到∠ABC=EBD,由BC平分∠EBD,得到∠ABE=∠EBC=∠CBD,根据平角定义,即可得到答案;
(2)由(1)知,∠EBC=∠CBD=60°,由三角形外角定理可得,![]() 则
则![]() 即可得到结论成立.
即可得到结论成立.
(1)解:由旋转的性质,得:∠ABC=∠EBD,
即![]() ,
,
∴∠ABE=∠CBD,
∵BC平分∠EBD,
∴∠EBC=∠CBD,
∴∠ABE=∠EBC=∠CBD,
∵∠ABE+∠EBC+∠CBD=180°,
∴∠CBD=60°.
(2)证明:如图,BE与AC相交与点P,DE与AC相交与点F,

由(1)知,∠EBC=∠CBD=60°,
由三角形外角定理,得:∠APB=∠EBC+∠C=60°+∠C,∠CBD=∠A+∠C=60°,
∴∠APB=∠A+2∠C
∴∠APB>∠A,结论成立.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目