题目内容
3. 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于点A(1,6),B(3,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于点A(1,6),B(3,n)两点.(1)求反比例函数和一次函数的表达式;
(2)点M是一次函数y=kx+b图象位于第一象限内的一点,过点M作MN⊥x轴,垂足为点N,过点B作BD⊥y轴,垂足为点D,若△MON的面积小于△BOD的面积,直接写出点M的横坐标x的取值范围.
分析 (1)把A(1,6)代入y=$\frac{m}{x}$即可求出反比例函数的表达式,把B(3,n)代入y=$\frac{6}{x}$即可求出B的坐标,把A、B的坐标代入y=kx+b,求出a、b,即可求出一次函数的表达式;
(2)求出直线和x轴的交点坐标,根据面积得出关于x的不等式,求出不等式的解集即可.
解答 解:(1)把A(1,6)代入y=$\frac{m}{x}$得:m=6,
即反比例函数的表达式为y=$\frac{6}{x}$,
把B(3,n)代入y=$\frac{6}{x}$得:n=2,
即B的坐标为(3,2),
把A、B的坐标代入y=kx+b得:$\left\{\begin{array}{l}{k+b=6}\\{3k+b=2}\end{array}\right.$,
解得:k=-2,b=8,
即一次函数的表达式为y=-2x+8;
(2)
设直线y=2x+8与x轴交于C点,
∵M在直线y=-2x+8上,
∴M的坐标为(x,-2x+8),则MN=-2x+8,ON=x,
则C的坐标为(4,0),
即OC=4,
∵B(3,2),
∴OD=3,BD=2,SBOD=$\frac{1}{2}$×OD×BD=3,
∵△MON的面积小于△BOD的面积,
∴$\frac{1}{2}•x•(-2x+8)$<3,
整理得:x2-4x+3>0,
解得:x<1或x>3,
∵M点在第一象限,OC=4,
∴0<x<1或3<x<4,
当△MON的面积小于△BOD的面积时,点M的横坐标x的取值范围是0<x<1或3<x<4.
点评 本题考查了一次函数与反比例函数的交点问题,用待定系数法求出函数的解析式,二次函数的性质等知识点,能正确用待定系数法求出函数的解析式是解此题的关键.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
13.阿伟的游戏机充满电后,可用来连续播放音乐36个小时或连续玩游戏6个小时,若游戏机在早上7点充满电后,阿伟马上使用游戏机播放音乐直到下午3点,并从下午3点继续使用游戏机玩游戏直到它没电,则他的游戏机何进没电?( )
| A. | 晚上7点20分 | B. | 晚上8点20分 | C. | 晚上7点40分 | D. | 晚上8点40分 |
14.下面是一位同学做的四道题:
①2a+3b=5ab;
②-(-2a2b3)4=-16a8b12;
③(a+b)3=a3+b3;
④(a-2b)2=a2-2ab+4b2
其中做对的一道题的序号是( )
①2a+3b=5ab;
②-(-2a2b3)4=-16a8b12;
③(a+b)3=a3+b3;
④(a-2b)2=a2-2ab+4b2
其中做对的一道题的序号是( )
| A. | ① | B. | ② | C. | ③ | D. | ④ |
11.下列各式中,计算过程正确的是( )
| A. | $\sqrt{{2^2}+{7^2}}$=2+7 | B. | $\sqrt{9\frac{1}{2}}$=3$\sqrt{\frac{1}{2}}$ | C. | $\sqrt{6}$÷$\sqrt{3}$=$\sqrt{2}$ | D. | $\frac{{\sqrt{8}+\sqrt{12}}}{{\sqrt{2}}}$=4+6 |
18.下列四个命题:①坐标平面内的点与有序数对一一对应;②若a大于0,b不大于0,则点P(-a,-b)在第三象限;③在x轴上的点的纵坐标都为0;④当m=0时,点P(m2,-m)在第四象限.其中,是真命题的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.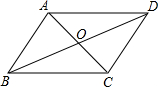 如图,四边形ABCD的对角线AC,BD相交于点O,欲使ABCD为平行四边形,需添加条件( )
如图,四边形ABCD的对角线AC,BD相交于点O,欲使ABCD为平行四边形,需添加条件( )
 如图,四边形ABCD的对角线AC,BD相交于点O,欲使ABCD为平行四边形,需添加条件( )
如图,四边形ABCD的对角线AC,BD相交于点O,欲使ABCD为平行四边形,需添加条件( )| A. | AB=AD,BC=CD | B. | AO=OC,BO=DO | C. | AO⊥OD | D. | AO⊥AB |
12.将直线y=2x-4向上平移5个单位长度后,所得直线的表达式是( )
| A. | y=2x-9 | B. | y=2x-5 | C. | y=2x+5 | D. | y=2x+1 |
13.若(m-3)0=1,则m的取值为( )
| A. | m=3 | B. | m≠3 | C. | m<3 | D. | m>3 |