题目内容
 阅读理解.
阅读理解.已知,如图①,∠A+∠AEC+∠C=360°.求证:AB∥CD.
证明:过点E作EF∥AB.
∴∠A+∠AEF=180°(两直线平行,同旁内角互补)
∵∠A+∠AEC+∠C=360°(已知)
即∠A+∠AEF+∠CEF+∠C=360°
∴∠CEF+∠C=360°-(∠A+∠AEF)=360°-180°=180°
∴EF∥CD(同旁内角互补,两直线平行)
∵EF∥AB(辅助线作法)
∴AB∥CD(如果两条直线都与第三条直线平行,那么这两条直线也互相平行)
象EF这样为了解题需要而添画的线叫辅助线.请按照上面的方法解题:
已知,如图②,∠A+∠C=∠AEC.
求证:AB∥CD.
考点:平行线的判定与性质
专题:阅读型
分析:过E作EF∥AB,根据两直线平行,内错角相等,可以证得∠A=∠AEF,则∠C=∠CEF证明EF∥CD,根据平行于同一直线的两直线平行即可证得.
解答: 证明:过E作EF∥AB,
证明:过E作EF∥AB,
∵EF∥AB,
∴∠A=∠AEF,
又∵∠A+∠C=∠AEC,
∴∠C=∠CEF,
∴EF∥CD,
又∵EF∥AB,
∴AB∥CD.
 证明:过E作EF∥AB,
证明:过E作EF∥AB,∵EF∥AB,
∴∠A=∠AEF,
又∵∠A+∠C=∠AEC,
∴∠C=∠CEF,
∴EF∥CD,
又∵EF∥AB,
∴AB∥CD.
点评:本题考查了平行线的判定与性质,解题的关键是正确作出辅助线,然后根据两直线平行内错角相等的性质解此类题.

练习册系列答案
相关题目

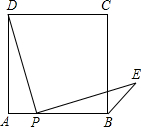 点P是正方形ABCD边AB上一点(不与A,B重合),连接PD并将线段PD绕点P顺时针旋转90°,得到线段PE,连接BE,则∠CBE等于
点P是正方形ABCD边AB上一点(不与A,B重合),连接PD并将线段PD绕点P顺时针旋转90°,得到线段PE,连接BE,则∠CBE等于 如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)6米的点A处,沿OA所在直线行走14米到点B时(即AB=14米),人影长度增加了
如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)6米的点A处,沿OA所在直线行走14米到点B时(即AB=14米),人影长度增加了