题目内容
17. 如图,AB是⊙0的直径,AB=10,C、D是⊙O上的点,∠CDB=30°,过点C作⊙O的切线交AB的延长线于E,则OE等于多少?
如图,AB是⊙0的直径,AB=10,C、D是⊙O上的点,∠CDB=30°,过点C作⊙O的切线交AB的延长线于E,则OE等于多少?
分析 连接OC.由同弧所对的圆心角是圆周角的2倍可求得∠COB=60°,然后由切线的性质可证明∠CCE=90°,根据三角形的内角和是180°可求得∠CEO=30°,依据含30°直角三角形的性质可知OE=2OC.
解答 解:连接OC.
∵∠CDB=30°,
∴∠COB=60°.
∵CE是⊙O的切线,
∴∠CCE=90°.
∴∠CEO=30°.
∴OE=2OC=AB=10.
点评 本题主要考查的是切线的性质、圆周角定理、含30°直角三角形的性质,证得△OCE为含30°的直角三角形是解题的关键.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案
相关题目
15.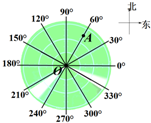 一艘海上搜救船借助雷达探测仪寻找到事故船的位置,雷达示意图如图所示,搜救船位于图中圆心O处,事故船位于距O点40海里的A处,雷达操作员要用方向角把事故船相对于搜救船的位置汇报给船长,以便调整航向,下列四种表述方式中正确的为( )
一艘海上搜救船借助雷达探测仪寻找到事故船的位置,雷达示意图如图所示,搜救船位于图中圆心O处,事故船位于距O点40海里的A处,雷达操作员要用方向角把事故船相对于搜救船的位置汇报给船长,以便调整航向,下列四种表述方式中正确的为( )
 一艘海上搜救船借助雷达探测仪寻找到事故船的位置,雷达示意图如图所示,搜救船位于图中圆心O处,事故船位于距O点40海里的A处,雷达操作员要用方向角把事故船相对于搜救船的位置汇报给船长,以便调整航向,下列四种表述方式中正确的为( )
一艘海上搜救船借助雷达探测仪寻找到事故船的位置,雷达示意图如图所示,搜救船位于图中圆心O处,事故船位于距O点40海里的A处,雷达操作员要用方向角把事故船相对于搜救船的位置汇报给船长,以便调整航向,下列四种表述方式中正确的为( )| A. | 事故船在搜救船的北偏东60°方向 | B. | 事故船在搜救船的北偏东30°方向 | ||
| C. | 事故船在搜救船的北偏西60°方向 | D. | 事故船在搜救船的南偏东30°方向 |
9. 实数a在数轴上的位置如图所示,则化简|1-a|+$\sqrt{(a-2)^{2}}$的结果是( )
实数a在数轴上的位置如图所示,则化简|1-a|+$\sqrt{(a-2)^{2}}$的结果是( )
 实数a在数轴上的位置如图所示,则化简|1-a|+$\sqrt{(a-2)^{2}}$的结果是( )
实数a在数轴上的位置如图所示,则化简|1-a|+$\sqrt{(a-2)^{2}}$的结果是( )| A. | -1 | B. | 1 | C. | 2a-3 | D. | 3-2a |
7.下列运算正确的是( )
| A. | x6÷x3=x2 | B. | (-2x)3=-8x3 | C. | x6•x4=x24 | D. | (x3)3=x6 |