题目内容
11.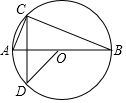 如图,AB是⊙O的直径,点C在⊙O上,连接AC、BC,过点O作OD∥AC交⊙O于点D,点C、D在AB的异侧,若∠B=24°,则∠BCD的度数是( )
如图,AB是⊙O的直径,点C在⊙O上,连接AC、BC,过点O作OD∥AC交⊙O于点D,点C、D在AB的异侧,若∠B=24°,则∠BCD的度数是( )| A. | 66° | B. | 67° | C. | 57° | D. | 48° |
分析 先求出∠A,得出∠AOD,由等腰三角形的性质和三角形内角和定理求出∠OAD,再由圆周角定理求出∠BCD的度数即可.
解答 解:连接AD,如图所示:
∵AC∥OD,
∴∠A=∠AOD,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠A=90°-∠B=66°.
∴∠AOD=66°,
∵OA=OD,
∴∠OAD=(180°-∠AOD)÷2=57°,
∴∠BCD=∠OAD=57°;
故选:C.
点评 本题考查了圆周角定理、平行线的性质,熟练掌握圆周角定理的内容是解题关键.

练习册系列答案
相关题目
1.二次函数y=ax2+bx+c中,y与x的部分对应值如下表:
根据表格,小明得出三个结论:①ac<0;②当x=2时,y=5;③x=3是方程ax2+(b-1)x+c=0的一个根,其中结论正确的共有( )
| x | -1 | 0 | 1 | 3 |
| y | -1 | 3 | 5 | 3 |
| A. | 0 个 | B. | 1个 | C. | 2个 | D. | 3个 |
2.下列长度的三条线段能组成三角形的是( )
| A. | 3,2,1 | B. | 3,2,5 | C. | 3,4,6 | D. | 3,4,7 |
6.若宇宙中一块陨石落在地球上,它落在陆地上的概率是0.3,那么用扇形统计图反映地球上陆地面积与海洋面积所占的比例时,陆地面积所对应的圆心角是( )
| A. | 54° | B. | 72° | C. | 108° | D. | 114° |
16.下列每组数分别是三根木棒的长度,不能用它们摆成三角形的是( )
| A. | 5cm、8cm、12cm | B. | 6cm、8cm、12cm | C. | 5cm、6cm、8cm | D. | 5cm、6cm、12cm |
3.如图,把一个长方形的纸片按图所示对折两次,然后剪下三角形展开,得到的四边形一定是( )

| A. | 正方形 | B. | 菱形 | ||
| C. | 矩形 | D. | 仅有一组对边平行的四边形 |
20.一个数用科学记数法表示为2.37×105,则这个数是( )
| A. | 237 | B. | 2370 | C. | 23700 | D. | 237000 |
1.在平行四边形、正方形、圆、菱形、正六边形中,既是轴对称图形又是中心对称图形的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |