题目内容
2.把下列各式因式分解:(1)-12a2b+24ab2;
(2)8a(x-y)2-4b(y-x);
(3)2(a-3)2-a+3;
(4)(a+b)2+(a+b)(a-3b);
(5)(x2+3x)-3(x+3);
(6)$\frac{1}{2}$a2(x-2a)2-$\frac{1}{4}$a(2a-x)3.
分析 (1)根据提取公因式-12ab,可分解因式;
(2)根据提取公因式4(x-y),可分解因式;
(3)根据提取公因式(a-3),可分解因式;
(4)根据提取公因式(a+b),可分解因式;
(5)根据提取公因式(x+3),可分解因式;
(6)根据提取公因式$\frac{1}{2}$a(x-2a)2,可分解因式.
解答 解:(1)原式=-12ab(a-2b)
(2)原式=4(x-y)[2a(x-y)+b]=4(x-y)(2ax-2ay+b);
(3)原式=(a-3)[2(a-3)-1]=(a-3)(2a-4)=2(a-3)(a-2);
(4)原式=(a+b)[(a+b)-(a-3b)]=4b(a+b);
(5)原式=(x+3)(x-3);
(6)原式=$\frac{1}{2}$a(x-2a)2[a+$\frac{1}{2}$(x-2a)]=$\frac{1}{2}$a(x-2a)2($\frac{1}{2}$x)=$\frac{1}{4}$ax(x-2a)2.
点评 本题考查了因式分解,提取公因式分解因式,确定公因式是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.$\frac{1}{4}$的倒数是( )
| A. | -$\frac{1}{4}$ | B. | -4 | C. | $\frac{1}{4}$ | D. | 4 |
17.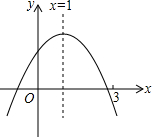 二次函数y=ax2+bx+c(a≠0)图象如图所示.下列结论中,错误的是( )
二次函数y=ax2+bx+c(a≠0)图象如图所示.下列结论中,错误的是( )
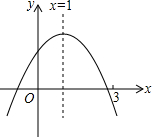 二次函数y=ax2+bx+c(a≠0)图象如图所示.下列结论中,错误的是( )
二次函数y=ax2+bx+c(a≠0)图象如图所示.下列结论中,错误的是( )| A. | abc<0 | |
| B. | 当m≠1时,a+b>am2+bm | |
| C. | 2a+b=0 | |
| D. | 若ax12+bx1=ax22+bx2且x1≠x2,x1+x2=3 |
 在一次抽奖活动中,主办方将奖品随机的放在如图所示的黑白相间的正方形小窗后,如果这次抽奖共分三等,其中一等奖1个,二等奖2相,三等奖3个,那么第一个抽奖人推开一扇黑色小窗能够得到一等奖奖品的概率为$\frac{1}{21}$.
在一次抽奖活动中,主办方将奖品随机的放在如图所示的黑白相间的正方形小窗后,如果这次抽奖共分三等,其中一等奖1个,二等奖2相,三等奖3个,那么第一个抽奖人推开一扇黑色小窗能够得到一等奖奖品的概率为$\frac{1}{21}$.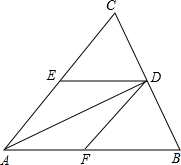 如图,AD是△ABC的角平分线,DE∥AB,DF∥AC,分别交AC,AB于点E,F.若∠EAD=20°,求∠EDF的度数.
如图,AD是△ABC的角平分线,DE∥AB,DF∥AC,分别交AC,AB于点E,F.若∠EAD=20°,求∠EDF的度数.