题目内容
【题目】如图，在Rt△ABC中，∠C=90°，AC=10，BC=15，点D，E，P分别是边AC，AB；BC上的点，且AD=4，AE=4EB．若
是等腰三角形，则CP的长是__________．
【答案】
或
【解析】
建立如图平面直角坐标系,，表示出D（0，6）P（x，0）E（12，2），利用长度公式进行分类讨论即可．
建立如图平面直角坐标系
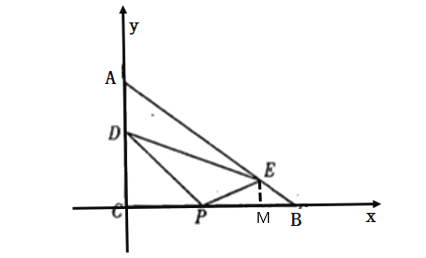
∵AC=10,AD=4
∴
∴
∵过E作EM⊥BC于M
∴EM∥AC
∴
∴BM=3，EM=2
∴CM=12
∴E（12，2）
设P（x，0）
∵AD=4，AC=10
∴CD=6
∵D（0，6）P（x，0）E（12，2）
∴
，
，
当DE=PD时，
∴
∴
∴
∴CP=
当DE=PE时，
∴
∴
（负值舍去）
∴
>CB
∵P是边BC上的点
∴当DE=PE时，不符合题意；舍去
当DP=PE时，
∴
∴
∴CP=
故答案为： 或
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
