题目内容
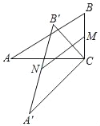
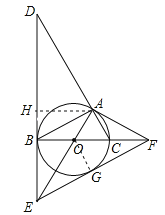
【题目】已知：在菱形ABCD中，O是对角线BD上的一动点．
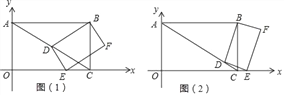
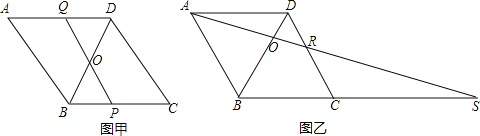
（1）如图甲，P为线段BC上一点，连接PO并延长交AD于点Q，当O是BD的中点时，求证：
；
（2）如图乙，连接AO并延长，与DC交于点R，与BC的延长线交于点
若
，
，
，求AS和OR的长．
【答案】（1）见解析；（2）
，
.
【解析】
（1）根据菱形的性质证明△ODQ≌△OBP，即可得到
．
（2）首先求AS的长，要通过构建直角三角形求解；过A作BC的垂线，设垂足为T，在Rt△ABT中，易证得∠ABT=∠DCB=60°，又已知了斜边AB的长，通过解直角三角形可求出AT、BT的长；进而可在Rt△ATS中，由勾股定理求出斜边AS的值；由于四边形ABCD是菱形，则AD∥BC，易证得△ADO∽△SBO，已知了AD、BS的长，根据相似三角形的对应边成比例线段可得出OA、OS的比例关系式，即可求出OA、OS的长；同理，可通过相似三角形△ADR和△SCR求得AR、RS的值；由OR=OS-RS即可求出OR的长．
（1）证明：
四边形ABCD为菱形，
．
,
是BD的中点，
,
在
和
中，
，
，
≌
．
（2）解：如图乙，
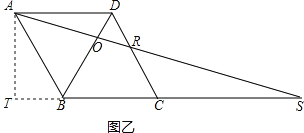
过A作
，与CB的延长线交于T．
是菱形，
，
在
中，
,
，
，
在
中，
．
，
∽
．
，
则
，
，
，
．
同理可得
∽
．
，
则
，
，
．
．
练习册系列答案
全优点练单元计划系列答案
相关题目
