Question

【题目】已知如图是边长为10的等边△ABC．

（1）作图：在三角形ABC中找一点P，连接PA、PB、PC，使△PAB、△PBC、△PAC面积相等．（不写作法，保留痕迹．）

（2）求点P到三边的距离和PA的长．

Answer 1

【答案】（1）见解析；（2）点P到三边的距离为：，PA=.

【解析】

（1）依据△PAB、△PBC、△PAC面积相等，可得点P为△ABC的内心，作△ABC的内角平分线，交点P即为所求；

（2）依据∠DBP=30°，∠ADB=90°，BD=BC=5，即可得到点P到三边的距离为，进而得出AP=AD-PD=.

（1）如图所示，点P即为所求；

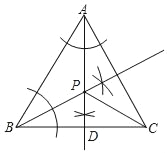
（2）由（1）可得，点P为△ABC的内角平分线的交点，

∴∠DBP＝30°，∠ADB＝90°，BD＝BC＝5，

∴PD＝tan30°×BD＝，

∴点P到三边的距离为，

∵Rt△ABD中，AD＝tan60°×BD＝5，

∴AP＝AD﹣PD＝5﹣＝．