题目内容
16.在△ABC中,点D,E分别在边AB,AC上,AD=BD,AE=2EC.设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,那么$\overrightarrow{DE}$=$\frac{2}{3}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$(用$\overrightarrow{a}$、$\overrightarrow{b}$的式子表示)分析 首先根据题意画出图形,然后由在△ABC中,点D,E分别在边AB,AC上,AD=BD,AE=2EC,求得$\overrightarrow{AD}$与$\overrightarrow{AE}$,再利用三角形法则求解即可求得答案.
解答 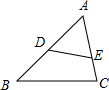 解:如图,∵在△ABC中,点D,E分别在边AB,AC上,AD=BD,AE=2EC,
解:如图,∵在△ABC中,点D,E分别在边AB,AC上,AD=BD,AE=2EC,
∴$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{AB}$=$\frac{1}{2}$$\overrightarrow{a}$,$\overrightarrow{AE}$=$\frac{2}{3}$$\overrightarrow{AC}$=$\frac{2}{3}$$\overrightarrow{b}$,
∴$\overrightarrow{DE}$=$\overrightarrow{AE}$-$\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$.
故答案为:$\frac{2}{3}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$.
点评 此题考查了平面向量的知识.注意三角形法则的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.右图是某几何体的三视图,该几何体是( )


| A. | 圆柱 | B. | 正方体 | C. | 圆锥 | D. | 长方体 |
7.若点M(x,y)满足x+y=0,则点M位于( )
| A. | 第一、三象限两坐标轴夹角的平分线上 | |
| B. | x轴上 | |
| C. | 第二、四象限两坐标轴夹角的平分线上 | |
| D. | y轴上 |
4.下列各数中与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{2}$ | B. | $\root{3}{2}$ | C. | $\sqrt{4}$ | D. | $\sqrt{12}$ |
1.下面计算正确的是( )
| A. | a+a-1=0 | B. | ($\sqrt{2}$+1)(1-$\sqrt{2}$)=1 | C. | (xy)-1($\frac{1}{2}$xy)2=$\frac{1}{4}$xy | D. | -(-a)4÷a2=a2 |
5.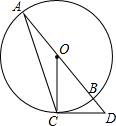 如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,连接OC,AC.若∠D=50°,则∠A的度数是( )
如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,连接OC,AC.若∠D=50°,则∠A的度数是( )
 如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,连接OC,AC.若∠D=50°,则∠A的度数是( )
如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,连接OC,AC.若∠D=50°,则∠A的度数是( )| A. | 20° | B. | 25° | C. | 40° | D. | 50° |
 如图,△AED∽△ACB,△AED的面积为△ACB面积的$\frac{1}{3}$,则AD:AB=$\sqrt{3}$:3.
如图,△AED∽△ACB,△AED的面积为△ACB面积的$\frac{1}{3}$,则AD:AB=$\sqrt{3}$:3.