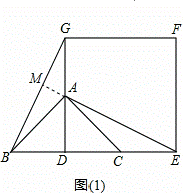
题目内容
如图(1),已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点.作正方形DEFG,使点A、C分别在DG和DE上,连接AE、BG.
(1)试猜想线段BG和AE的关系(位置关系及数量关系),请直接写出你得到的结论:
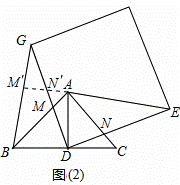
(2)将正方形DEFG绕点D逆时针方向旋转一角度a后(0°<a<90°),如图(2),通过观察或测量等方法判断(1)中的结论是否仍然成立?如果成立,请予以证明;如果不成立,请说明理由:
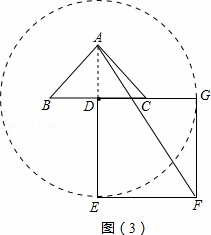
(3)若BC=DE=m,正方形DEFG绕点D逆时针方向旋转角度a(0°<a<360°)过程中,当AE为最大值时,求AF的值.
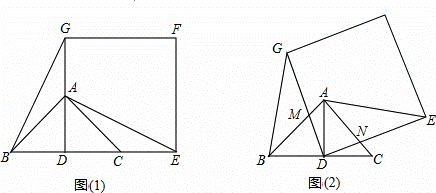
解:(1)如图(1),
∵△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点,
∴BD=CD=AD,
∵在△BDG和△ADE中
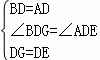 ,
,
∴△BDG≌△ADE(SAS),
∴BG=AE,∠DGB=∠DEA,
延长EA到BG于一点M,
∴∠GAM=∠DAE,
∴∠GMA=∠EDA=90°,
∴线段BG和AE相等且垂直;
(2)成立,
如图(2),延长EA分别交DG、BG于点M′、N′两点,
∵△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点,
∴∠ADB=90°,且BD=AD,
∵∠BDG=∠ADB﹣∠ADG=90°﹣∠ADG=∠ADE,
∵在△BDG和△ADE中
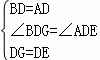 ,
,
∴△BDG≌△ADE(SAS),
∴BG=AE,∠DEA=∠DGB,
∵∠DEA+∠DNE=90°,∠DNE=∠MNG,
∴∠MNG+∠DGM=90°,
即BG⊥AE且BG=AE;
(3)由(2)知,要使 AE最大,只要将正方形绕点D逆时针旋旋转270°,即A,D
AE最大,只要将正方形绕点D逆时针旋旋转270°,即A,D ,E在一条直线上时,AE最大;
,E在一条直线上时,AE最大;
∵正方形DEFG在绕点D旋转的过程中,E点运动的图形是以点D为圆心,DE为半径的圆,
∴当正方形DEFG旋转到G点位于BC的延长线上(即正方形DEFG绕点D逆时针方向旋转270°)时,BG最大,如图(3),
若BC=DE=m,则AD=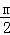 ,EF=m,
,EF=m,
在Rt△AEF中,AF2=AE2+EF2=(AD+DE)2+EF2=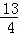 m2,
m2,
∴AF=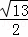 m,即在正方形DEFG旋转过程中,当AE为最大值时,AF=
m,即在正方形DEFG旋转过程中,当AE为最大值时,AF=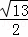 m.
m.

 比例尺是1:8000的某市地图上,若一条路的长度约25cm,则它的实际长度约为
比例尺是1:8000的某市地图上,若一条路的长度约25cm,则它的实际长度约为 天空气质量指数实时查询的一个结果.
天空气质量指数实时查询的一个结果.
 (x>0)的图象经过顶点B,则k的值为__________.
(x>0)的图象经过顶点B,则k的值为__________.
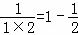
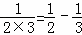
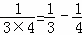
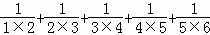 =_
=_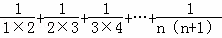 =__________;(用含有n的式子表示)
=__________;(用含有n的式子表示)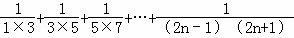 的值为
的值为 ,求n的值.
,求n的值. 的图象在第一象限相交于点A,与x轴相交于点C,AB⊥x轴于点B,△AOB的面积为1,则AC的长为__________(保留根号).
的图象在第一象限相交于点A,与x轴相交于点C,AB⊥x轴于点B,△AOB的面积为1,则AC的长为__________(保留根号).