题目内容
 如图,AC=
如图,AC=| 1 |
| 3 |
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:两点间的距离
专题:计算题
分析:设AB=12a,则AC=
AB=4a,BD=
AB=3a,则CD=AB-AC-DB=5a,而AE=CD,则AE=5a,于是利用CE=AE-AC可得CE=a,然后计算CE:AB即可.
| 1 |
| 3 |
| 1 |
| 4 |
解答:解:设AB=12a,
∵AC=
AB,
∴AC=4a,
∵BD=
AB,
∴BD=3a,
∴CD=AB-AC-DB=12a-4a-3a=5a,
∵AE=CD,
∴AE=5a,
∴CE=AE-AC=5a-4a=a,
∴CE=
AB.
故选C.
∵AC=
| 1 |
| 3 |
∴AC=4a,
∵BD=
| 1 |
| 4 |
∴BD=3a,
∴CD=AB-AC-DB=12a-4a-3a=5a,
∵AE=CD,
∴AE=5a,
∴CE=AE-AC=5a-4a=a,
∴CE=
| 1 |
| 12 |
故选C.
点评:本题考查了两点间的距离:连接两点间的线段的长度叫两点间的距离.距离是一个量,有大小,区别于线段,线段是图形.线段的长度才是两点的距离.会利用代数法解决求线段长的问题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
在直线上取三点A、B、C,使线段AB=8cm,BC=3cm,则线段AC的长( )
| A、11cm | B、5cm |
| C、11cm或5cm | D、7cm |
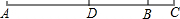 如图,延长线段AB到点C,使BC=
如图,延长线段AB到点C,使BC= 如图,将△ABC绕点O旋转,使顶点A与点A′重合,画出旋转后的图形.
如图,将△ABC绕点O旋转,使顶点A与点A′重合,画出旋转后的图形. 如图,△ABC中,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.EF=6,BE=4,则CF的长为( )
如图,△ABC中,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.EF=6,BE=4,则CF的长为( )