题目内容
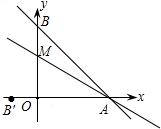如图，A、B两点坐标分别是（4，0），（0，3），M是y轴上一点，沿AM折叠，AB刚好落在x轴上AB′处，则直线AM的解析式为________．
y=-
x+
分析：连接B′M，利用勾股定理求得OM的长，也就求得了M的坐标，进而用待定系数法求直线解析式即可．
解答：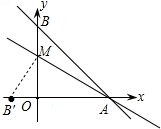
解：易得AB=5，
∴AB′=5，
∴OB′=1，
由折叠可得BM=B′M，
∴OM2+OB′2=B′M2，即OM2+12=（3-OM）2，
解得OM=．
设AM的解析式为y=kx+，
∴4k+=0，
解得k=-，
∴y=-x+．
故答案为y=-x+．
点评：综合考查一次函数的相关问题；利用勾股定理得到OM的长是解决本题的突破点．
x+分析：连接B′M，利用勾股定理求得OM的长，也就求得了M的坐标，进而用待定系数法求直线解析式即可．
解答：
解：易得AB=5，∴AB′=5，
∴OB′=1，
由折叠可得BM=B′M，
∴OM2+OB′2=B′M2，即OM2+12=（3-OM）2，
解得OM=
．设AM的解析式为y=kx+
，∴4k+
=0，解得k=-
，∴y=-
x+．故答案为y=-
x+．点评：综合考查一次函数的相关问题；利用勾股定理得到OM的长是解决本题的突破点．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，A、B两点坐标分别是（4，0），（0，3），M是y轴上一点，沿AM折叠，AB刚好落在x轴上AB′处，则直线AM的解析式为
如图，A，B两点坐标分别是A（2| 3 |
| 3 |
A、
| ||
| B、3 | ||
C、2
| ||
| D、6 |
如图：A、B两点坐标分别为（8，0）和（4，3），P点在y轴上且以O、A、B、P为顶点的四边形为梯形，则P点坐标为
如图：A，B两点坐标分别为A（