题目内容
4．当m＜-1时，分式$\frac{2}{{x}^{2}-2x-m}$无论x取何值都有意义．分析 分式总有意义，即分母不等于0，即当分母等于0时，对应的方程无解．
解答 解：根据题意得：x2-2x-m=0中，
△=4+4m＜0．
解得：m＜-1．
故答案是：＜-1．
点评 本题考查了分式有意义的条件以及二次方程有解的条件，转化为一元二次方程的解的问题是关键．
练习册系列答案
相关题目
12．通分：
（1）$\frac{1}{{a}^{2}b}$，$\frac{1}{a{b}^{2}}$；
（2）$\frac{2}{{x}^{2}+x}$，$\frac{4}{3{x}^{2}-6x}$．
（1）$\frac{1}{{a}^{2}b}$，$\frac{1}{a{b}^{2}}$；
（2）$\frac{2}{{x}^{2}+x}$，$\frac{4}{3{x}^{2}-6x}$．
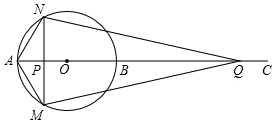已知：如图，AB为⊙O的直径，点C为AB延长线上一点，动点P从点A出发沿AC方向以1cm/s的速度运动，同时动点Q从点C出发以相同的速度沿CA方向运动，当两点相遇时停止运动，过点P作AB的垂线，分别交⊙O于点M和点N，已知⊙O的半径为2，AC=10，设运动时间为ts．
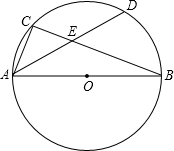如图，AB为⊙O的直径，C为⊙O上一点，弦AD平分∠BAC，交BC于点E，AB=10，AD=8，则AE的长为$\frac{7}{2}$．
4．若a＞b，则下列结论正确的是（ ）
| A． | a2＞b2 | B． | a2＜b2 | ||
| C． | a2≥b2 | D． | a2与b2的大小关系不能确定 |