题目内容
12.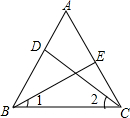 如图,在等边△ABC中,DE分别是AB,AC上的点,且AD=CE.
如图,在等边△ABC中,DE分别是AB,AC上的点,且AD=CE.(1)求证:BE=CD;
(2)求∠1+∠2的度数.
分析 (1)根据等边三角形的性质得出∠A=∠ACB=60°,AC=BC,根据SAS推出△ACD≌△CBE,即可得出答案;
(2)根据全等得出∠1=∠ACD,求出∠1+∠2=∠ACB.即可得出答案.
解答 (1)证明:∵△ABC是等边三角形,
∴∠A=∠ACB=60°,AC=BC,
在△ACD和△CBE中
$\left\{\begin{array}{l}{AC=BC}\\{∠A=∠BCE}\\{AD=CE}\end{array}\right.$
∴△ACD≌△CBE(SAS),
∴BE=CD;
(2)解:∵△ACD≌△CBE,
∴∠1=∠ACD,
∴∠1+∠2=∠ACD+∠2=∠ACB=60°.
点评 本题考查了全等三角形的性质和判定,等边三角形的性质的应用,能求出△ACD≌△CBE是解此题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
7. 把如图所示的平面图形绕直线L旋转一周,得到的立体图形是( )
把如图所示的平面图形绕直线L旋转一周,得到的立体图形是( )
 把如图所示的平面图形绕直线L旋转一周,得到的立体图形是( )
把如图所示的平面图形绕直线L旋转一周,得到的立体图形是( )| A. | 圆柱 | B. | 圆锥 | C. | 球 | D. | 棱锥 |
17. 某人骑自行车从甲地到乙地,到达乙地他马上返回甲地.如图反映的是他离甲地的距离s(km)及他骑车的时间t(h)之间的关系,则下列说法正确的是( )
某人骑自行车从甲地到乙地,到达乙地他马上返回甲地.如图反映的是他离甲地的距离s(km)及他骑车的时间t(h)之间的关系,则下列说法正确的是( )
 某人骑自行车从甲地到乙地,到达乙地他马上返回甲地.如图反映的是他离甲地的距离s(km)及他骑车的时间t(h)之间的关系,则下列说法正确的是( )
某人骑自行车从甲地到乙地,到达乙地他马上返回甲地.如图反映的是他离甲地的距离s(km)及他骑车的时间t(h)之间的关系,则下列说法正确的是( )| A. | 甲、乙两地之间的距离为60km | |
| B. | 他从甲地到乙地的平均速度为30km/h | |
| C. | 当他离甲地15km时,他骑车的时间为1h | |
| D. | 若他从乙地返回甲地的平均速度为10km/h,则点A表示的数字为5 |


 如图,已知直线l1:y=x+3与x轴交于点A,与y轴交于点B,与直线l2:y=-$\frac{1}{2}$x交于点P.直线l3:y=-$\frac{3}{2}$x+4与x轴交于点C,与y轴交于点D,与直线l1交于点Q,与直线l2交于点R.
如图,已知直线l1:y=x+3与x轴交于点A,与y轴交于点B,与直线l2:y=-$\frac{1}{2}$x交于点P.直线l3:y=-$\frac{3}{2}$x+4与x轴交于点C,与y轴交于点D,与直线l1交于点Q,与直线l2交于点R.